Розв'яжіть рівняння:
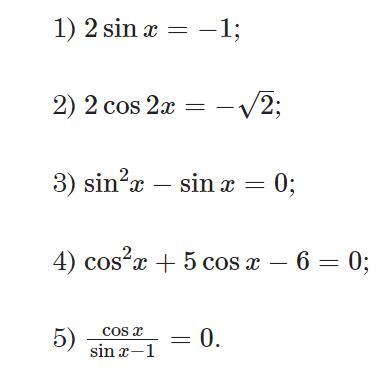
Ответы
Відповідь:
1) 2sinx = -1
sinx = -1/2
x = arcsin(-1/2) + 2πn, n є Z
x = π-arcsin(-1/2) + 2πn, n є Z
x = -π/6 + 2πn, n є Z
x = 7π/6 + 2πn, n є Z
2) 2cos2x = -√2
cos2x = -√2/2
2x = ± arccos(-√2/2) + 2πn, n є Z
2x = ±3π/4 + 2πn, n є Z
x = 3π/8 + 2πn, n є Z
x = π-3π/8 + 2πn, n є Z
x = 3π/8 + 2πn, n є Z
x = 5π/8 + 2πn, n є Z.
3) sin²x-sinx = 0
sinx(sinx-1) = 0
Об'єднання:
sinx = 0
sinx = 1
x = πn, n є Z
x = π/2 + 2πn, n є Z.
4) cos²x + 5cosx - 6 = 0
Позначимо cosx за t, тепер
t²+5t-6 = 0
За теоремою Вієта:
t1+t2 = -5
t1·t2 = -6
t1 = -6
t2 = 1
Звідси
cosx = -6 ( Оскільки cosx є [-1;1], x ∉ R)
cosx = 1
x = 2πn, n є Z
5) cosx/(sinx-1) = 0
Система:
cosx = 0
sinx-1 ≠ 0
x = π/2 + 2πn, n є Z
x = 3π/2 + 2πn, n є Z
x ≠ π/2 + 2πn, n є Z
Отже, x = 3π/2 + 2πn, n є Z.