Предмет: Алгебра,
автор: anhelinashaida2008
знайди область визначення функції
Приложения:
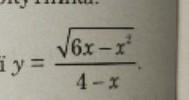
Ответы
Автор ответа:
0
Решение смотри на фото
Приложения:

Автор ответа:
0
Ответ:
Объяснение:
Из заданной функции мы видим, что
1) число под корнем всегда больше или равно нулю ⇒ 6x-x² ≥0
2) число в знаменателе никогда не равняется нулю ⇒ 4-х ≠ 0
Составляем ОДЗ:
Отдельно решим 1-ое уравнение системы
Вернёмся к системе
Похожие вопросы
Предмет: Математика,
автор: kataevakira930
Предмет: Математика,
автор: ketrin8794
Предмет: Алгебра,
автор: Аноним
Предмет: Химия,
автор: Yariktop2000yari
Предмет: Українська мова,
автор: melnichukkarina26777