Предмет: Алгебра,
автор: anyakulikova22
Решите,пожалуйста
Очень надо
Приложения:
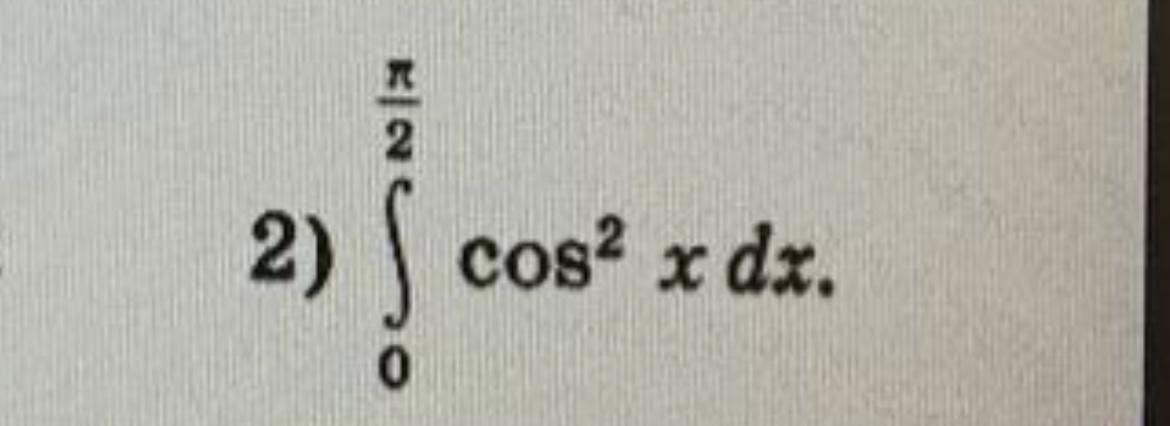
Ответы
Автор ответа:
2
Ответ:
π/4
Объяснение:
Определенный интеграл ищется по формуле Ньютона-Лейбница:
_____________
Преобразуем нашу функцию f(x) используя формулу понижения степени:
Находим определенный интеграл:
______________
Ещё применил формулу:
∫a dx = ax , где а - число
∫cosx dx = sinx
Похожие вопросы
Предмет: Экономика,
автор: dwrhzzhs8g
Предмет: Математика,
автор: irinaivchenko
Предмет: Математика,
автор: ramileiskenderova7
Предмет: История,
автор: Fgotu
Предмет: Химия,
автор: Vika111115898