Предмет: Математика,
автор: ilya23016
100 баллов
Решить уравнение и указать корни, принадлежащие отрезку
Желательно с решением
Приложения:
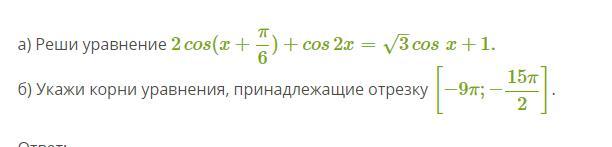
Ответы
Автор ответа:
2
Ответ:
-8π , -9π , -49π/6 , -53π/6
Пошаговое объяснение:
а)
Распишем cos(x+π/6) по формуле сложения аргументов: cos(α+β) = cosαcosβ - sinαsinβ
То есть:
Заменим cos2x = 1-2sin²x , тогда:
Получаем совокупность двух уравнений , причем , для удобства запишем корни не в общем виде:
б)
Сделаем отбор корней с помощью двойного неравенства:
Так как n∈Z , то нам подходит n = -9 , -8 .
Подставляем:
Уже два корня на указанном отрезке мы нашли , ищем дальше.
Нас устраивает k = -4 , подставим:
Осталось немного , ищем дальше:
Нам подходит m = -4 , следовательно:
Похожие вопросы
Предмет: Английский язык,
автор: rmotrus2
Предмет: Английский язык,
автор: Var4kar
Предмет: Алгебра,
автор: pikachyki1092
Предмет: Литература,
автор: cetverikovila4
Предмет: Химия,
автор: fedorcenkolmark78