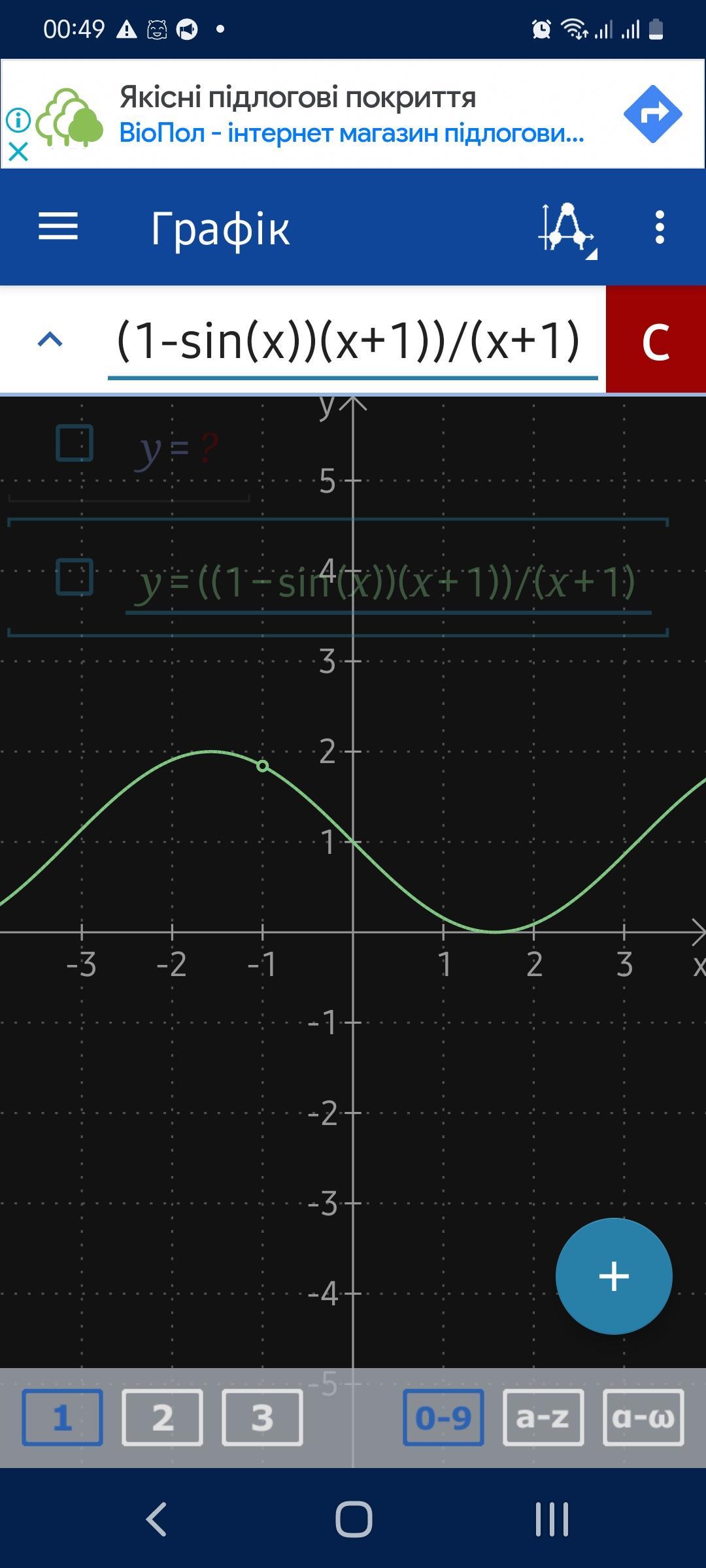
Дослідіть функцію на парність f(x)= ((1-sinx)*(x+1)) / (x+1)
Потрібне розвязання, будь ласка, не крадіть бали
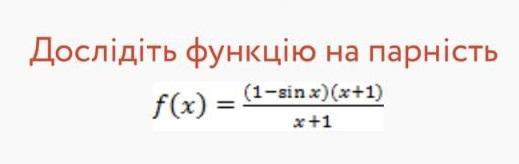
Ответы
Функція парності f(x) визначається як:
f(x) = ((1 - sin(x)) * (x + 1)) / (x + 1)
Щоб дослідити парність цієї функції, нам потрібно розглянути, чи є вона парною, непарною чи ні. Функція є парною, якщо f(-x) = f(x) для всіх x в області визначення функції. Функція є непарною, якщо f(-x) = -f(x) для всіх x в області визначення функції. Функція не є ні парною, ні непарною, якщо вона не задовольняє жодній із цих умов.
Щоб визначити парність цієї функції, ми можемо спростити вираз і використати властивості функції синус:
f(x) = ((1 - sin(x)) * (x + 1)) / (x + 1)
= (1 - sin(x))
Оскільки функція синус є непарною функцією, тобто sin(-x) = -sin(x), вираз можна спростити так:
f(x) = (1 - sin(x))
f(-x) = (1 - sin(-x))
= (1 + sin(x))
Як бачимо, f(-x) ≠ f(x), тому ця функція не є ні парною, ні непарною.
Отже, функція парності f(x) парна" це все виправити.
f(x) = ((1 - sin(x)) * (x + 1)) / (x + 1)
= (1 - sin(x))
Оскільки функція синус є непарною функцією, тобто sin(-x) = -sin(x), вираз можна спростити так:
f(x) = (1 - sin(x))
f(-x) = (1 - sin(-x))
= (1 + sin(x))
Як бачимо, f(-x) ≠ f(x), тому ця функція не є ні парною, ні непарною.
Відповідь: ні парна, ні непарна.
Пояснення:
Функцію у = f(x) називають парною, якщо її область визначення симетрична відносно нуля і для кожного х з області визначення виконується рівність f( -х) = f(х).
Функцію у = f(x) називають непарною, якщо її область визначення симетрична відносно нуля і для кожного х з області визначення виконується рівність f( -х) = -f(х).
Якщо область визначення не симетрична відносно нуля, то функція ні парна, ні непарна