Теорема про три перпендикуляри! Срочно!

Ответы
Ответ:
∠ВАЕ = ∠ВСЕ = 26°
Объяснение:
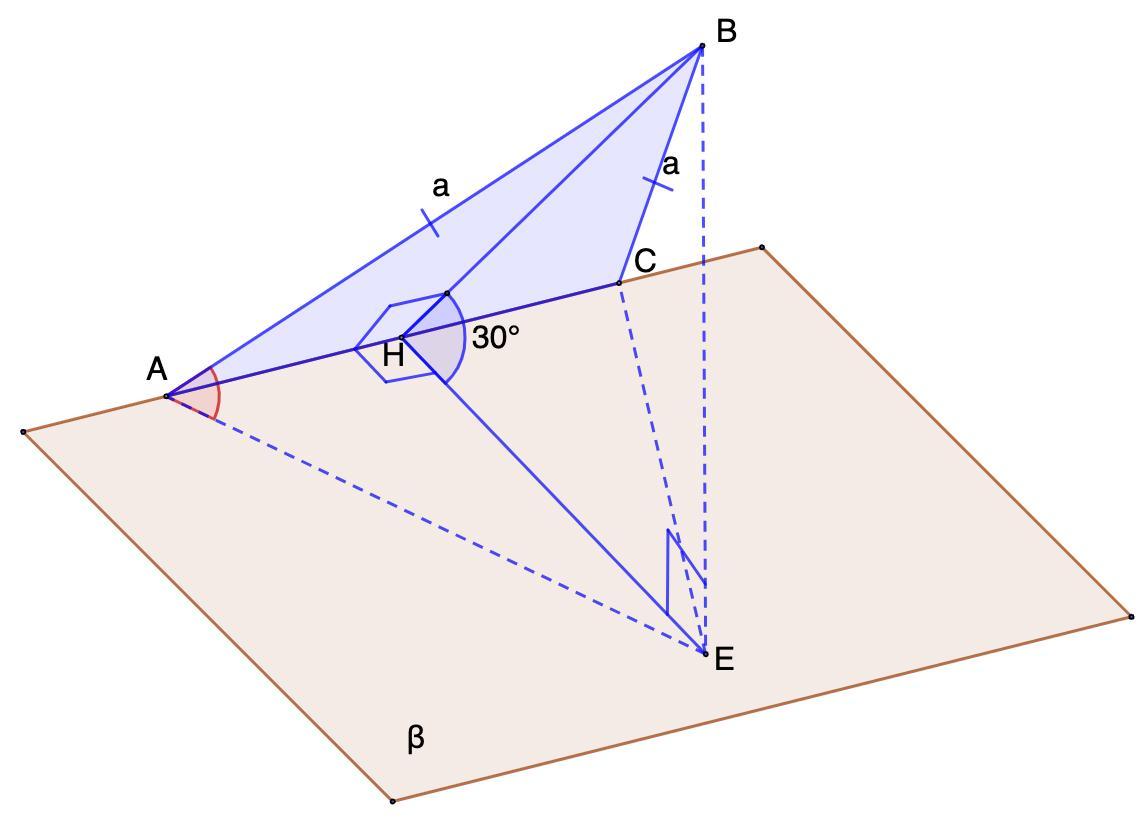
Через сторону правильного треугольника проведена плоскость, которая образует с плоскостью треугольника угол 30°. Найти углы, которые образуют две другие стороны треугольника с этой плоскостью.
Дано: ΔАВС - равносторонний;
(АВС) образует с β угол 30°.
Найти: углы, которые АВ и ВС с плоскостью β.
Решение:
- Угол между плоскостями – это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях.
Проведем ВН ⊥ АС. Опустим перпендикуляр ВЕ. Соединим Е и Н.
Прямая, проведенная на плоскости через основание наклонной перпендикулярно этой наклонной, перпендикулярна и ее проекции.
⇒ ЕН ⊥ АС
∠ВНЕ = 30° - угол между плоскостями.
1. Рассмотрим ΔАВН - прямоугольный.
Пусть АВ = а
2. Рассмотрим ΔНВЕ - прямоугольный.
- Катет, лежащий против угла в 30°, равен половине гипотенузы.
⇒
3. Рассмотрим ΔАВЕ - прямоугольный.
Угол между прямой и плоскостью — это угол между прямой и ее проекцией на данную плоскость.
∠ВАЕ ≈ 26°
4. Рассмотрим ΔАВЕ и ΔСВЕ - прямоугольные.
АВ = ВС; ВЕ - общая.
⇒ ΔАВЕ = ΔСВЕ (по гипотенузе и катету)
⇒ ∠ВАЕ = ∠ВСЕ = 26° (как соответственные элементы)