Предмет: Геометрия,
автор: skype32756328
Теорема про три перпендикуляри! Срочно!
Приложения:
Ответы
Автор ответа:
0
Ответ:
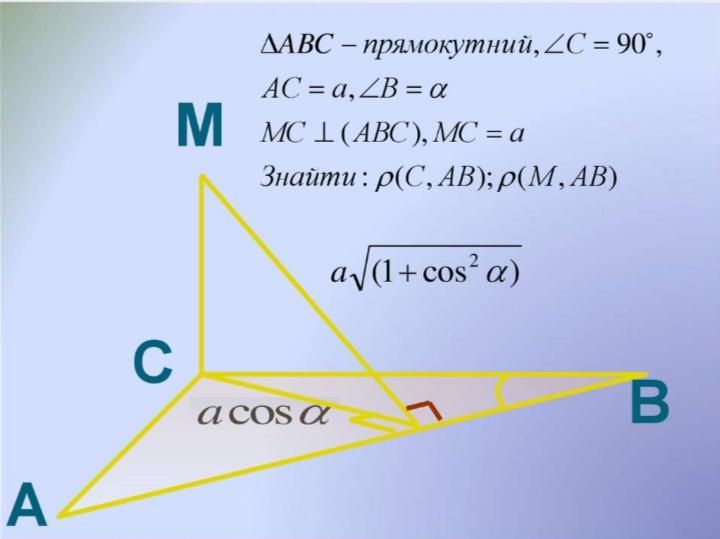
ρ(С, АВ) = a cosα
ρ(М; АВ) = a√(1+cos²α)
Объяснение:
Дано: ΔАВС - прямоугольный;
АС = а; ∠В = α;
МС ⊥ (АВС); МС = а
Найти: ρ(С, АВ); ρ(М; АВ)
Решение:
- Расстояние от точки до прямой - длина перпендикуляра, опущенного из данной точки на данную прямую.
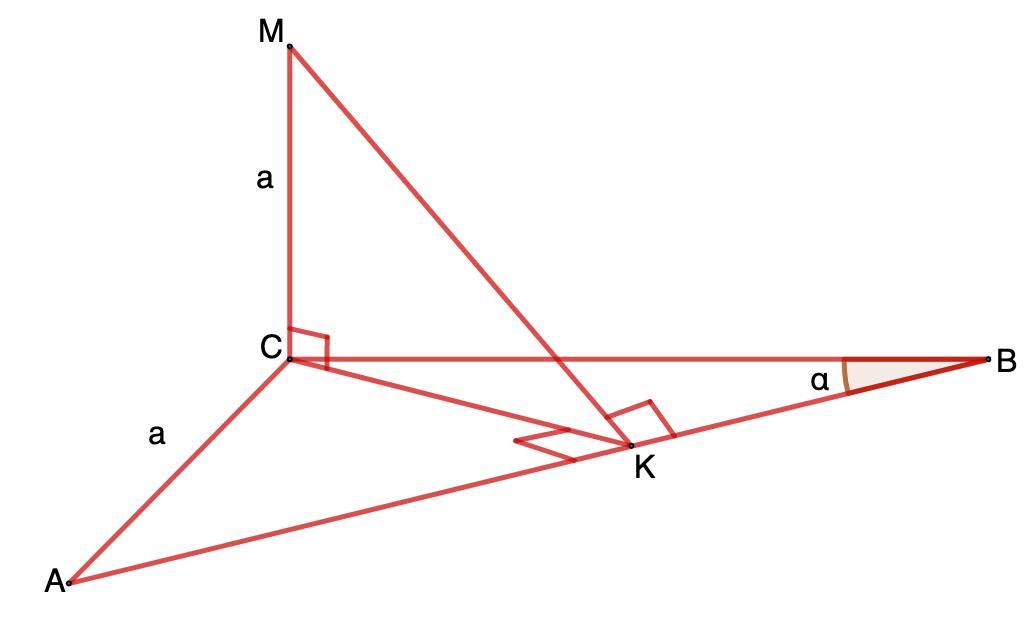
⇒ СК = ρ(С, АВ)
Рассмотрим ΔАСК - прямоугольный.
- Синус угла - отношение противолежащего катета к гипотенузе.
- Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠A = 90° - α
По формулам приведения
sin(90° - α) = cosα
CK = AC · sin(90° - α) = a cosα
ρ(С, АВ) = a cosα
2. Соединим К и М.
СМ ⊥ АВ ⇒ СК - проекция МК на (АВС)
- Прямая, проведенная на плоскости через основание наклонной перпендикулярно ее проекции, перпендикулярна и самой наклонной.
⇒ МК ⊥ АВ
МК = ρ(М; АВ)
СМ = а; СК = а cosα
По теореме Пифагора найдем МК:
МК² = СК² + СМ² = а²cos²α + a² = a²(1+cos²α) ⇒ MK = a√(1+cos²α)
ρ(М; АВ) = a√(1+cos²α)
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: tojieva2111
Предмет: Английский язык,
автор: s74863674
Предмет: Химия,
автор: shishova1992
Предмет: Математика,
автор: Аноним
Предмет: История,
автор: drilcuksofia