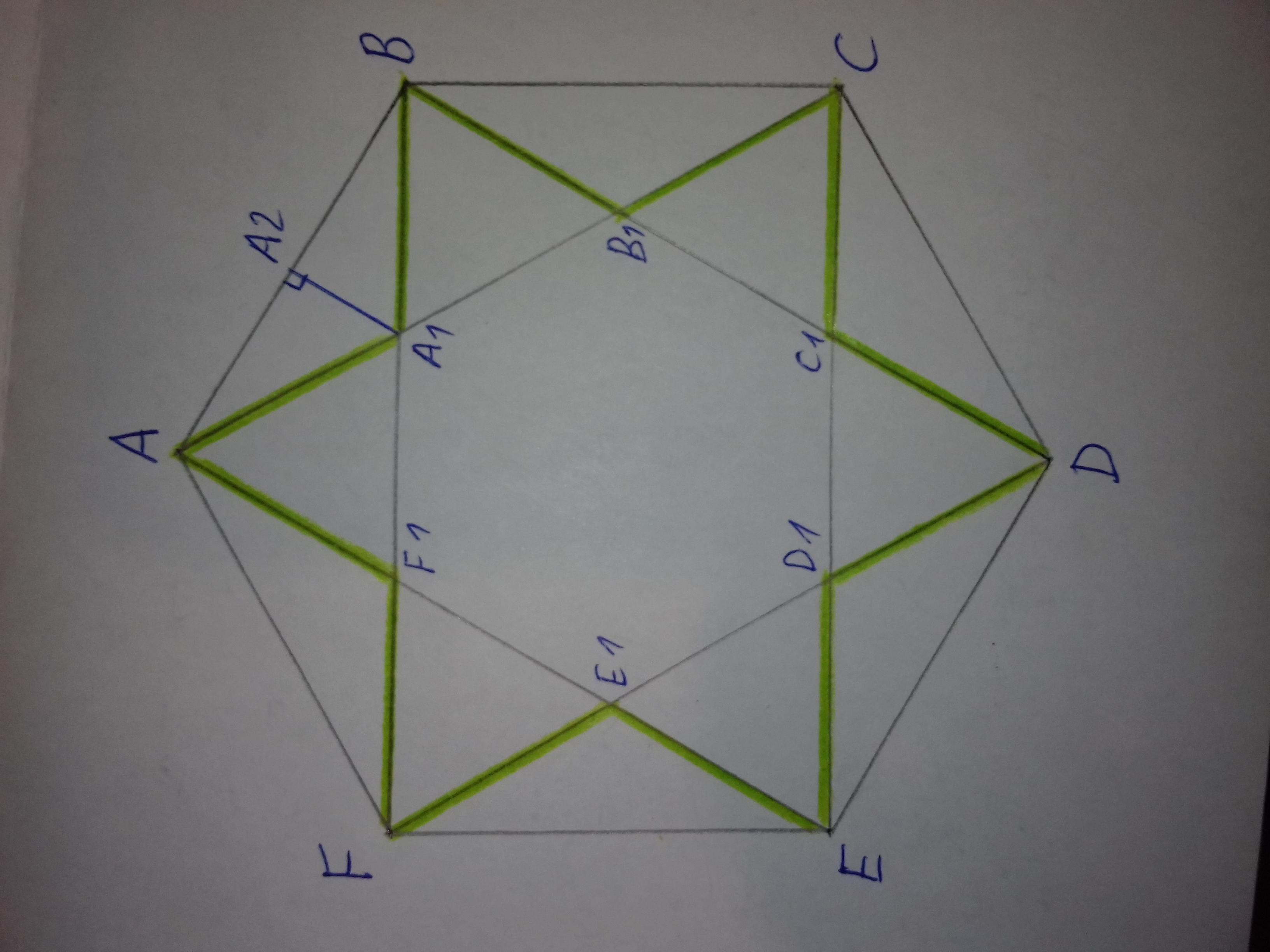
Проведемо короткі діагоналі правильного шестикутника, із яких утворився увігнутий многокутник ( із зеленими сторонами на малюнку )
Визнач периметр цього многокутника ( гексаграми ), якщо сторона правильного шестикутника складає 13 см
Відповідь : ...√....
Ответы
В силу симметрии построения зеленые отрезки равны.
Рассмотрим треугольник: основание - сторона шестиугольника, боковые стороны - зеленые отрезки. Равнобедренный, угол при основании 30° (вписанный угол, опирающийся на 1/6 окружности)
Зеленый отрезок = 13/2 :cos30° =13/2 :√3/2 =13/√3
P= 13/√3 *12 =52√3 (см)
Відповідь:
Периметр многокутника ( гексаграми ) дорівнює 52 × √3.
Пояснення:
Маємо правильний шестикутник ABCDEF всі сторони якого дорівнюють 13 см. Проведено короткі діагоналі AC, BD, CE, DF, EA, FB. В результаті утворився многокутник - гексаграма AA1BB1CC1DD1EE1FF1 ( дванадцятикутник із зеленими сторонами на малюнку ), що є шестикутною зіркою, що складена з двох рівносторонніх трикутників ACE та BDF, що мають спільний центр. Всі сторони гексаграми рівні між собою, тому її периметр дорівнює стороні помноженій на дванадцять.
Знайдемо довжину сторони гексаграми.
Розглянемо трикутник АВА1 - він рівнобедрений зі сторонами АА1 = ВА1.
Знайдемо ∠А1АВ = ( ∠FAB - ∠EAC ) / 2
∠FAB - внутрішній кут шестикутника ABCDEF. За правилом: Сума всіх внутрішніх кутів простого многокутника становить ( n - 2 ) × 180°, де n — кількість сторін.
Маємо n = 6
∑(внутр) = ( 6 - 2 ) × 180° = 4 × 180° = 720° Оскільки шестикутник ABCDEF - є правильним, то всі його внутрішні кути рівні між собою.
∠FAB = ∑(внутр) / 6 = 720° / 6 = 120°
∠EAC - внутрішній кут рівносторонього трикутника ACE. Сума всіх внутрішніх кутів трикутника дорівнює 180°. Оскільки трикутник ACE - є рівносторонім, то всі його внутрішні кути рівні між собою.
∠EAC = 180° / 3 = 60°
∠А1АВ = ( ∠FAB - ∠EAC ) / 2 = ( 120° - 60° ) / 2 = 60° / 2 = 30°
Таким чином трикутник АВА1 - рівнобедрений зі сторонами АА1 = ВА1, АВ = 13 см. ( за умовами задачі ) та кутами ∠А1АВ = ∠А1ВА = 30°
Проведемо А1А2 - перпендикуляр з точки А1 на відрізок АВ. За властивостями рівнобедреного трикутника висота А1А2, що проведена з вершини рівнобедреного трикутника до його основи є бісектрисою та висотою. Таким чином відрізки АА2 = А2В= АВ / 2 = 13 / 2 = 6,5 см. Утворилися два рівних прямокутних трикутника з ∠А1А2В = ∠А1А2А = 90°.
Розглянемо трикутник АА1А2.
Кут ∠А1АА2 = 30°
cos ( ∠А1АА2 ) = AA2 / AA1
Сторона АА1 = AA2 / cos ( ∠А1АА2 )
АА1 = 6,5 / ( √3 / 2 ) = 6,5 × 2 / √3 = 13 / √3
Периметр многокутника ( гексаграми ) дорівнює:
Р = 12 × АА1 = 12 × 13 / √3 = 156 / √3 = 52 × √3 × √3 / √3 = 52 × √3