Предмет: Геометрия,
автор: skype32756328
Теорема про три перпендикуляр! Терміново!
Приложения:
skype32756328:
А если 1) MF=BC?
В первом пункте доказать
Да. Можно попробовать
Ответы
Автор ответа:
2
Ответ:
Доказано, что MF ⊥ BC, МС = МА.
Объяснение:
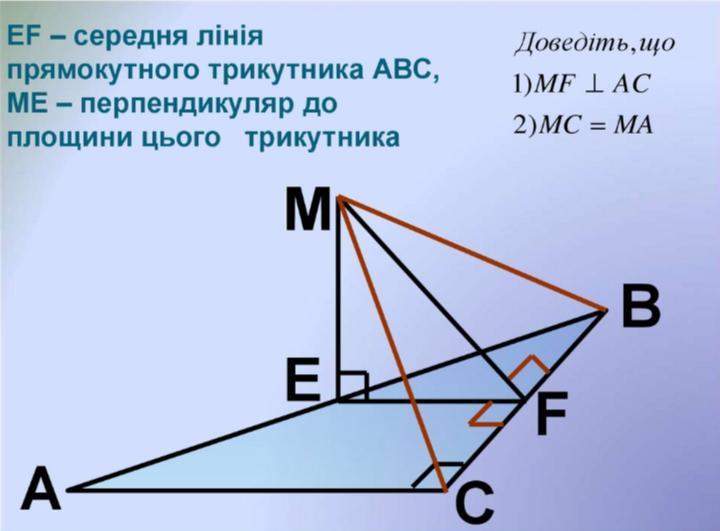
EF-средняя линия прямоугольного треугольника АВС, ME-перпендикуляр к плоскости этого треугольника.
Доказать: 1) MF ⊥ CB; 2) MC = MA.
Дано: ΔАВС - прямоугольный;
EF - средняя линия;
МЕ ⊥ АВС.
Доказать: МС = МА; MF ⊥ BC.
Доказательство:
1)
Рассмотрим ΔАВС - прямоугольный.
EF - средняя линия.
- Средняя линия параллельна стороне, которую она не пересекает.
⇒ EF || CB
- Если отрезок перпендикулярен одной из параллельных прямых, то он перпендикулярен и к другой прямой.
⇒ EF ⊥ CB
ME ⊥ ABC (условие)
⇒ EF - проекция MF на плоскость АВС.
- Теорема о трех перпендикулярах:
- Прямая, проведенная на плоскости через основание наклонной перпендикулярно ее проекции, перпендикулярна и самой наклонной.
⇒ MF ⊥ CB.
2)
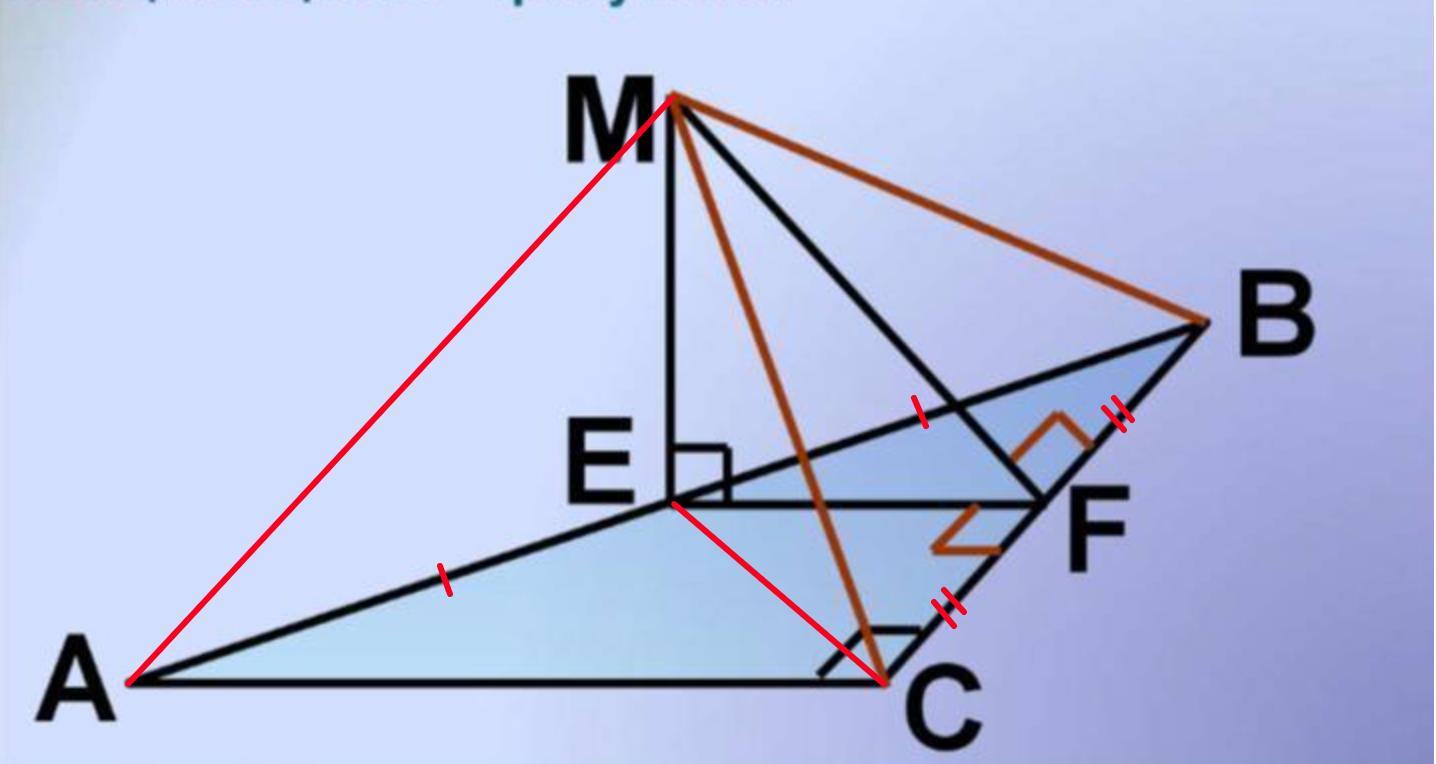
Соединим А и М, Е и С.
АЕ = ЕВ (ЕF - средняя линия)
⇒ СЕ - медиана.
- Медиана, проведенная из вершины прямого угла к гипотенузе равна ее половине.
⇒ СЕ = АЕ = ЕВ
- Если проекции наклонных, проведенных из одной точки равны, то и равны сами наклонные.
⇒ МС = МА.
Приложения:
Спасибо!
Похожие вопросы
Предмет: Физика,
автор: saidshaazizov
Предмет: Английский язык,
автор: arinovamedina3
Предмет: Информатика,
автор: durkinachasha2009
Предмет: Геометрия,
автор: anelaerkeskyzy
Предмет: Українська мова,
автор: AleksandrOksenchuk