Предмет: Геометрия,
автор: habikboom
4. Бісектриса гострого кута прямокутного трикутника ділить катет на
відрізки завдовжки 15 см і 25 см. Знайдіть периметр трикутника.
Ответы
Автор ответа:
2
Ответ:
Периметр треугольника равен 120 см
Объяснение:
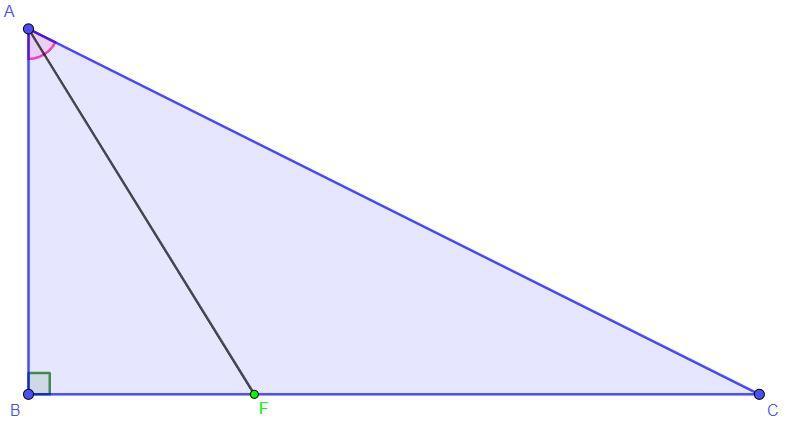
Дано: ∠ABC = 90°, AF - биссектриса, BF = 15 см, FC = 25 см
Найти:
Решение:
Рассмотрим треугольник ΔABC.
По основному свойству отрезка:
BC = BF + FC = 15 см + 25 см = 40 см
По теореме о биссектрисе треугольника (по условию AF - биссектриса):
По определению косинуса в прямоугольном треугольнике (по условию угол ∠ABC = 90°):
.
Значение произвольной функции от острого угла прямоугольного треугольника больше нуля по определению.
По основному тригонометрическому тождеству:
.
По определению синуса угла прямоугольного треугольника:
см.
По следствию из теоремы Пифагора:
см.
По определению периметра треугольника:
см.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: stella4694
Предмет: Математика,
автор: mikita998
Предмет: Литература,
автор: mtovkalov5238
Предмет: ОБЖ,
автор: EndlessPain0Katran