Предмет: Алгебра,
автор: history200802
Два приклади даю 100 балів
Розв'язати систему нерівностей.
Приложения:
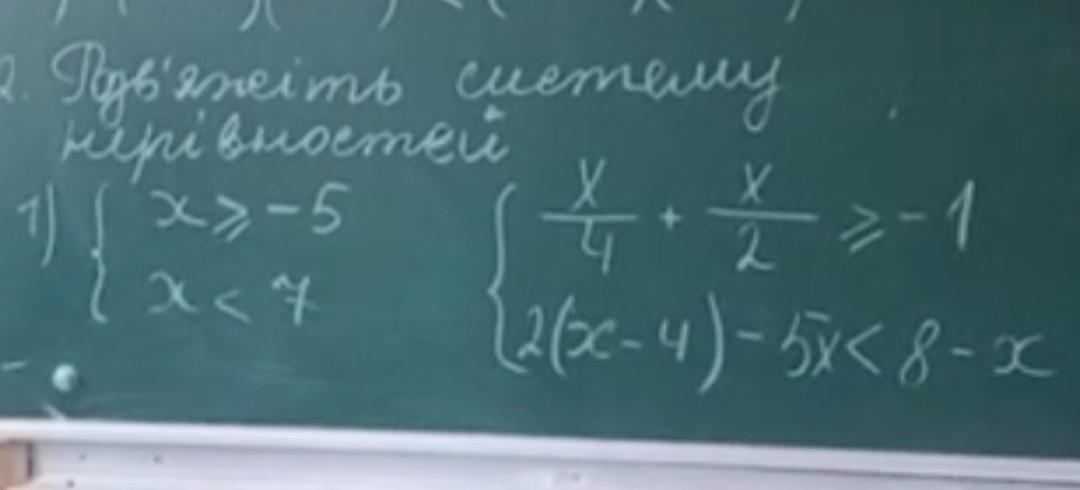
Ответы
Автор ответа:
0
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
-------------[ - 5]----------------(7)-----------
/////////////////////////////////////
Похожие вопросы
Предмет: Алгебра,
автор: a9799027
Предмет: Геометрия,
автор: georgiikolesnichenko
Предмет: Физика,
автор: georgiikolesnichenko
Предмет: Русский язык,
автор: extracreepycat
Предмет: Математика,
автор: Аноним