Предмет: Алгебра,
автор: Viscount
Решите второй столбик неравенств
Приложения:
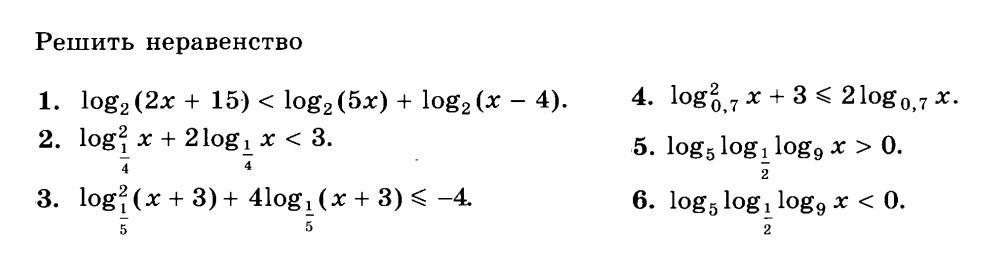
Ответы
Автор ответа:
1
Ответ:
4) x∈∅
5) x∈(1;3)
6) x∈(3;9)
Объяснение:
Вспомним определение логарифма и формулу арифметического квадратного корня:
,где a≠1 , a>0 , b>0.
______________
Одз: x>0
Пусть , тогда:
Следовательно , уравнение не имеет корней.
Найдем ОДЗ:
Приступаем к решению:
Найдя пересечение с Одз мы получим ответ :
Отличие с предыдущим примером только в знаках , одз мы уже знаем:
Сделав пересечение c Одз , ответом будет :
Похожие вопросы
Предмет: Физика,
автор: Jenakosmos
Предмет: Физика,
автор: Jenakosmos
Предмет: Химия,
автор: myravei1212
Предмет: Литература,
автор: kirill22890q
Предмет: Математика,
автор: trotsyk96