Предмет: Алгебра,
автор: ograt23
знайдіть значення виразу : 10 класс
Приложения:
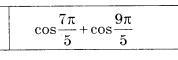
Ответы
Автор ответа:
0
Дополнительное пояснение :
Похожие вопросы
Предмет: Математика,
автор: anna518996g
Предмет: Математика,
автор: shaxlouralova1804
Предмет: Алгебра,
автор: leshukov19851918
Предмет: Физика,
автор: Shokorat
Предмет: История,
автор: IceCreamBear