Question

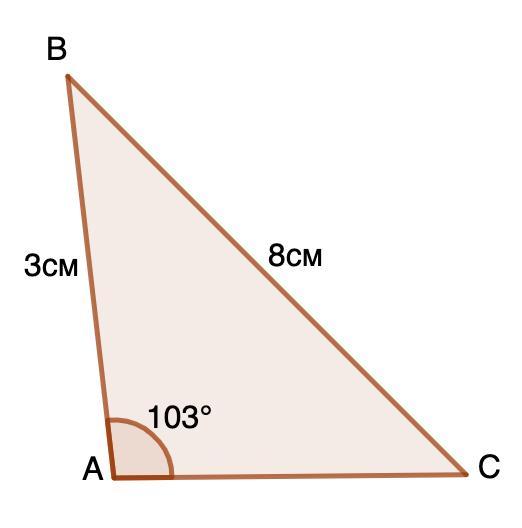
Знайдіть (з точністю до 1°) невідомі кути трикутника АВС, у якого АВ = 3 дм; ВС = 8 дм: <A=103.​

Answer 1

Ответ:

Угол С равен 21°, угол В равен 56°.

Объяснение:

Найдите (с точностью до 1°) неизвестные углы треугольника АВС, у которого АВ = 3 дм; ВС = 8 дм;  ∠A=103°.​

Дано: ΔАВС;

АВ = 3 дм; ВС = 8 дм;

∠A=103°

Найти: ∠В; ∠С.

Решение:

• Теорема синусов:
• Стороны треугольника пропорциональны синусам противолежащих углов.

$\displaystyle \frac{AB}{sin\;C}=\frac{BC}{sin\;A} =\frac{AC}{sin\;B}$

Подставим данные:

$\displaystyle \frac{3}{sin\;C}=\frac{8}{sin\;103^0} =\frac{AC}{sin\;B}$

Найдем ∠С

$\displaystyle \frac{3}{sin\;C}=\frac{8}{sin\;103^0} \\\\sin\;103^0\approx 0,97\\\\sin\;C=\frac{3\cdot0,97}{8}\approx 0,36\\ \\\angle C\approx 21^0$

• Сумма углов треугольника равна 180°.

⇒ ∠В = 180° - (∠А + ∠С) = 180° - (103° + 21°) = 56°

#SPJ1