Question

Точка F, не лежащая в плоскости треугольника MNT, равноудалена от его сторон, О – основание перпендикуляра, проведенного из точки F к плоскости треугольника. Точка О...
Даю 50 баллов, срочно, фото прикрепил

Answer 1

Ответ:

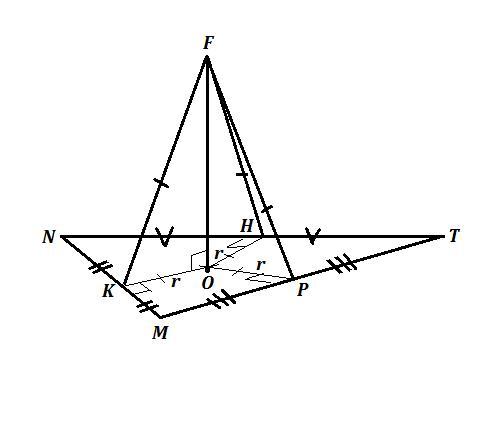
Точка F , не лежащая в плоскости  Δ MNT  , равноудалена от его сторон , то есть  FK=FP=FH , причём FК ⊥ MN ,  FР ⊥ MT ,  FН ⊥ NT .

Если из точки F опустить перпендикуляр на плоскость ΔMNT , то основанием перпендикуляра будет точка О .

Соединим точку О с точками К , Р  и Н .  Отрезки OК , OP , OH -  проекции наклонных FK , FP , FH . Они будут перпендикулярны сторонам треуг-ка по теореме о трёх перпендикулярах :ОК ⊥ MN ,  ОР ⊥ MT ,  ОН ⊥ NT , причём   OK=OP=OH  , так как равны сами наклонные .  

Значит,  OK ,OP и OH  - радиусы вписанной окружности.

Точки К , Р , Н - середины сторон треугольника : MK=KM , MP=PT , TH=HN  .

Точка О - центр вписанной в ΔMNT окружности , то есть - это пересечение серединных перпендикуляров в ΔMNT .