Предмет: Алгебра,
автор: kaseta345
решить интегралы (А,Б,В и соединить с вариантами 1,2,3,4)
Приложения:
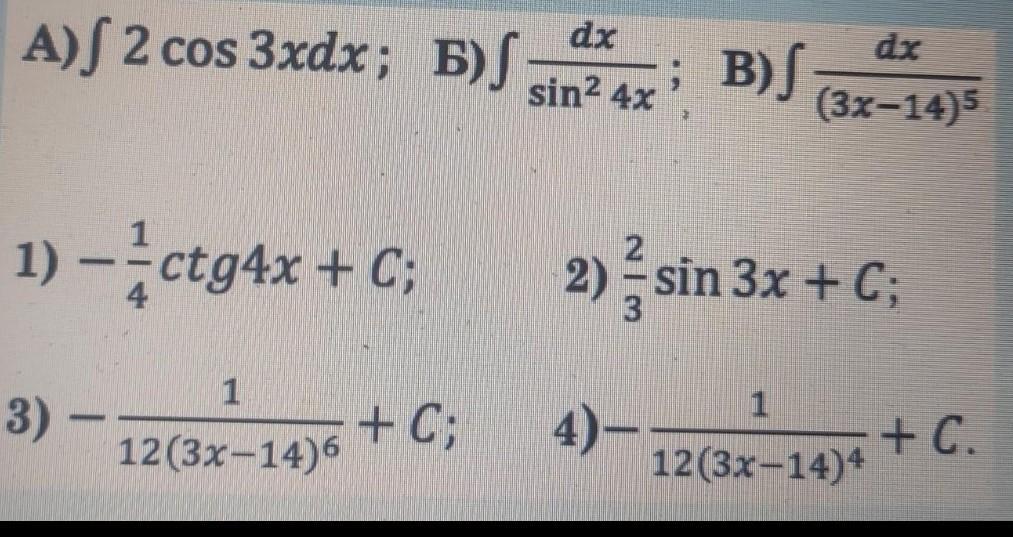
Ответы
Автор ответа:
2
Ответ.
Вычислить неопределённые интегралы (первообразную) . Применяем метод подведение под знак дифференциала (замены) .
Б)
Ответ: А - 2 , Б - 1 , В - 4 .
Похожие вопросы
Предмет: Английский язык,
автор: denjadenus2012
Предмет: Английский язык,
автор: gladinukmarta
Предмет: Математика,
автор: ajmanotargali780
Предмет: Математика,
автор: LindeX160