Предмет: Алгебра,
автор: Hdhdbdjhdsnk
СРОЧНО Помогите, нужно решить (b)
Приложения:
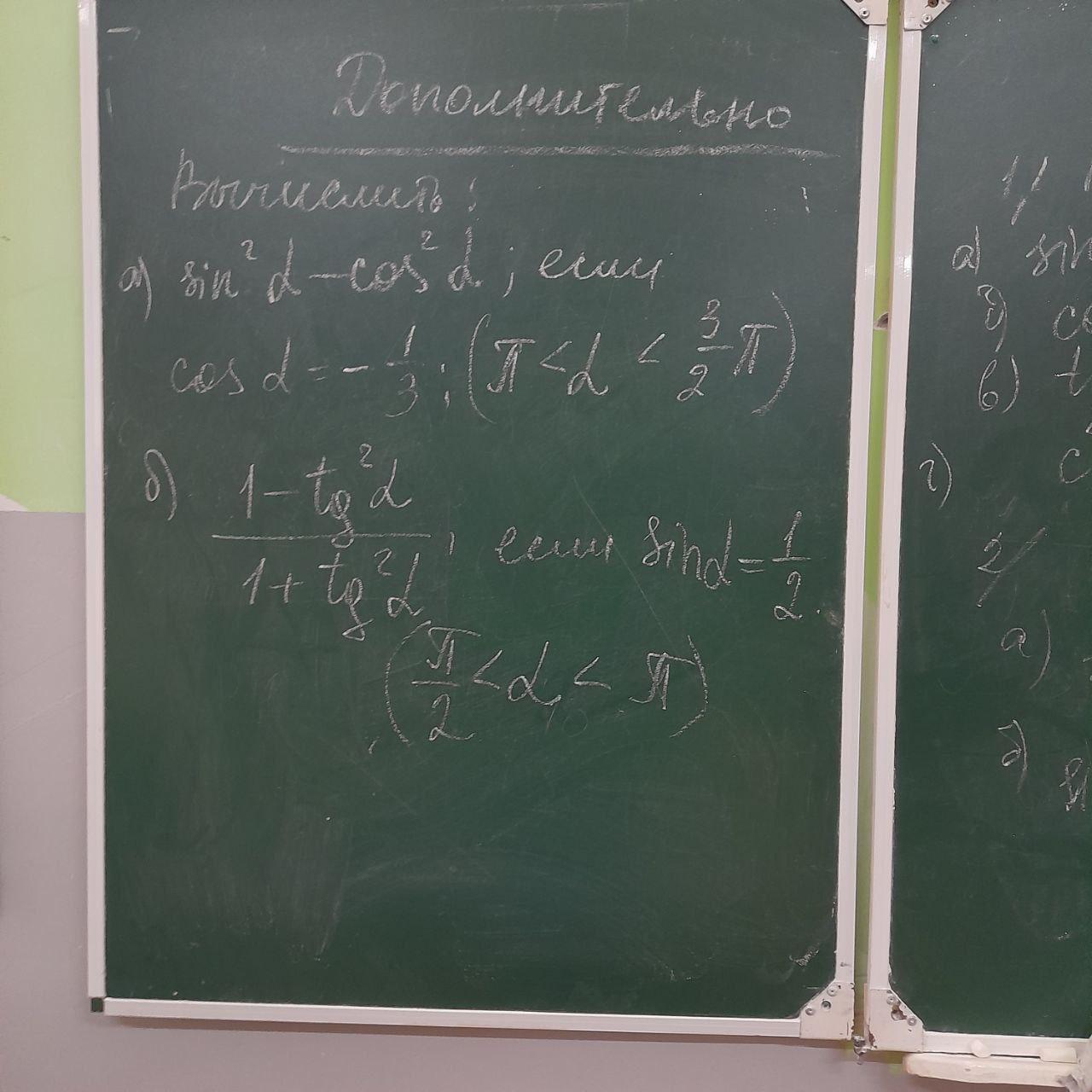
Ответы
Автор ответа:
3
Ответ:
Если , то из тождества
можно найти
.
Отсюда получим .
Так как , то
и получим
.
Вычислим значение дроби
Оказалось, что знак косинуса на результат не оказал влияния из-за того, что отрицательное число во второй степени есть число положительное .
Похожие вопросы
Предмет: Химия,
автор: aybek02
Предмет: Математика,
автор: maratjuo
Предмет: Математика,
автор: a98246767
Предмет: Русский язык,
автор: maruha3008
Предмет: Математика,
автор: topalev1999