Предмет: Алгебра,
автор: greka3456
Найти развязки системы уравнений
Даю 50 баллов
Приложения:
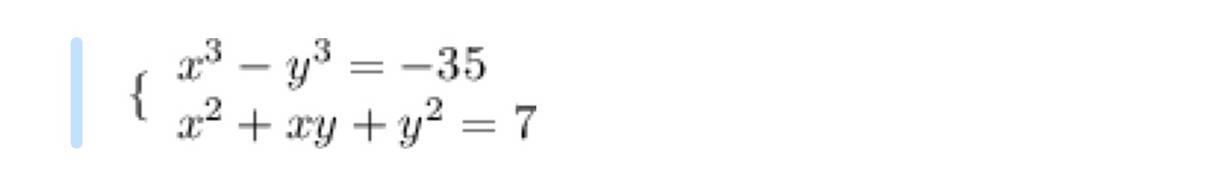
Ответы
Автор ответа:
2
Ответ:
(-2;3); (-3;2)
Объяснение:
Далее можно или выразить x через y и подставить во второе уравнение, или постараться воспользоваться теоремой Виета. Пойдем вторым путем. Препятствием служит только то, что нам дана не сумма корней, а их разность. Поэтому сделаем замену z= - y:
Следовательно x и z являются корнями уравнения
1-й случай: x=-2; z=-3⇒y=3.
2-й случай: x=-3; z=-2⇒y=2.
Похожие вопросы
Предмет: Химия,
автор: csgo3348
Предмет: Математика,
автор: lerakovalska21
Предмет: Математика,
автор: 14katya07
Предмет: Химия,
автор: mikhailpaly
Предмет: Химия,
автор: akosi8787