Предмет: Алгебра,
автор: debradixondixon
Алгебра 8 класс помогите пожалуйста даю 50 баллов
Приложения:
Ответы
Автор ответа:
0
Ответ:
.
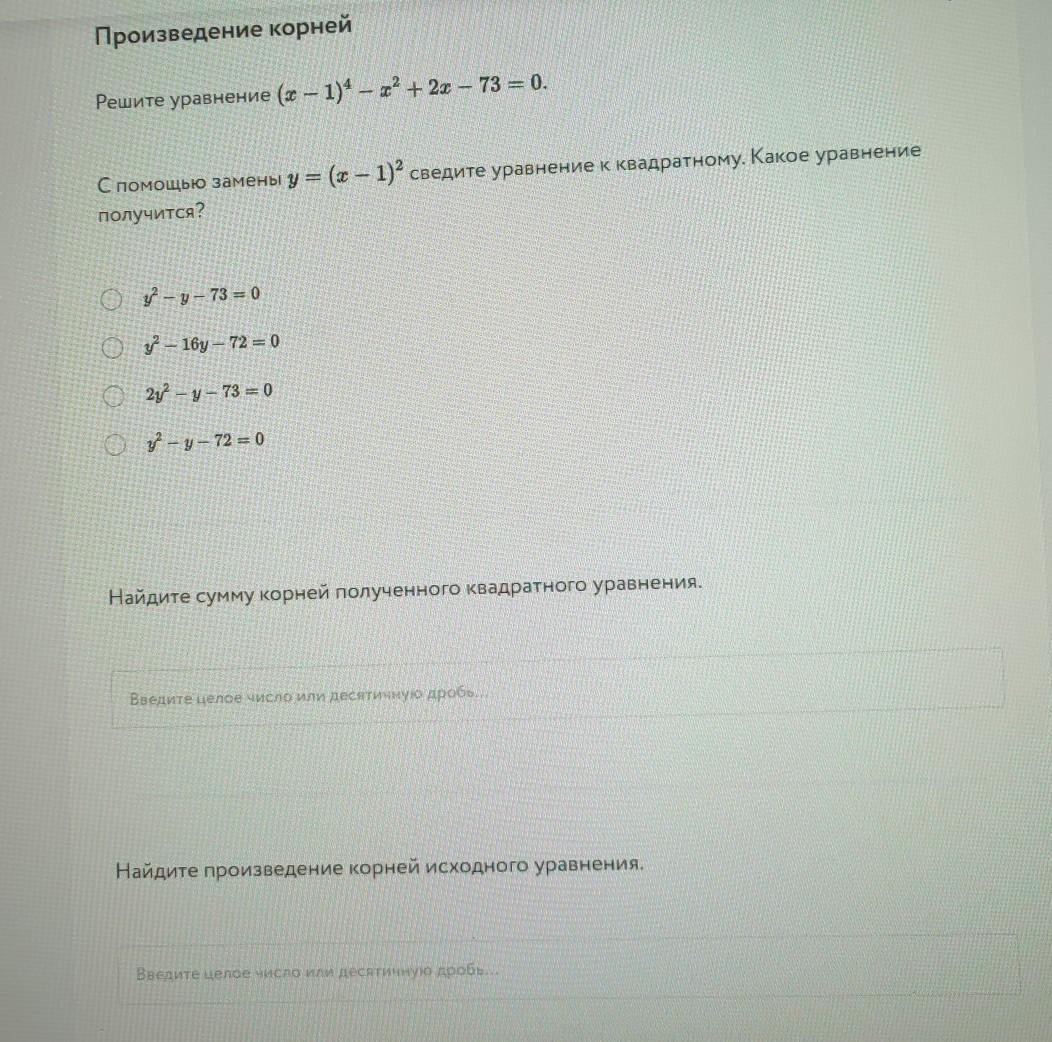
Получили уравнение №4 .
Сумма корней этого квадратного уравнения равна .
А произведение корней этого уравнения равно .
Поэтому корни полученного квадр. уравнения равны
Найдём корни исходного уравнения, учитывая, что .
Произведение корней исходного уравнения равно
Похожие вопросы
Предмет: Геометрия,
автор: ivangluho
Предмет: Алгебра,
автор: redted22893
Предмет: Математика,
автор: Аноним
Предмет: География,
автор: Аноним