Предмет: Алгебра,
автор: natali06071110
22.4. Упростите sin a cos a 1) 3) tga 1 1 - cos a выражение: - 1; 1 1 + cosa 2) 4) sin a cos a ctga 1 + tga 1 + ctga ; - 1;
Приложения:
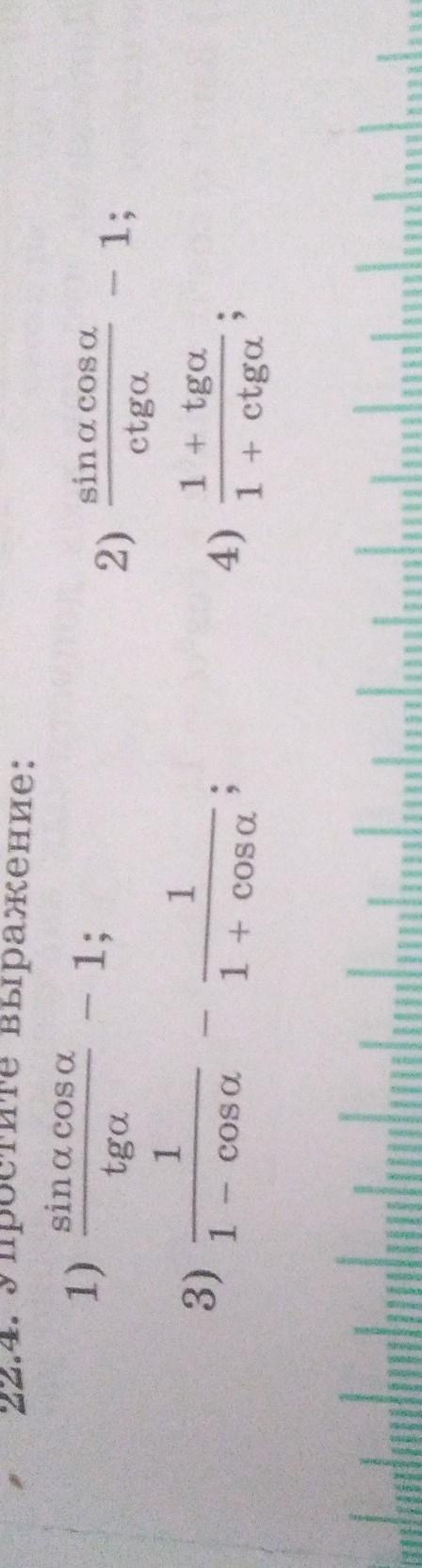
Ответы
Автор ответа:
6
Объяснение:
1) -sin²α
2) -cos²α
3) 2cosα/sin²α
4) tgα
Применим тригонометрические формулы:
Ещё формулу сокращенного умножения:
______________
Приложения:

natali06071110:
спасибо огромное. будем вникать
0_0
4 неправильнно
Похожие вопросы
Предмет: Английский язык,
автор: masichi
Предмет: Русский язык,
автор: firligmehmght
Предмет: Математика,
автор: sukhinetsangelina
Предмет: Геометрия,
автор: Аноним
Предмет: Математика,
автор: george1609