Question

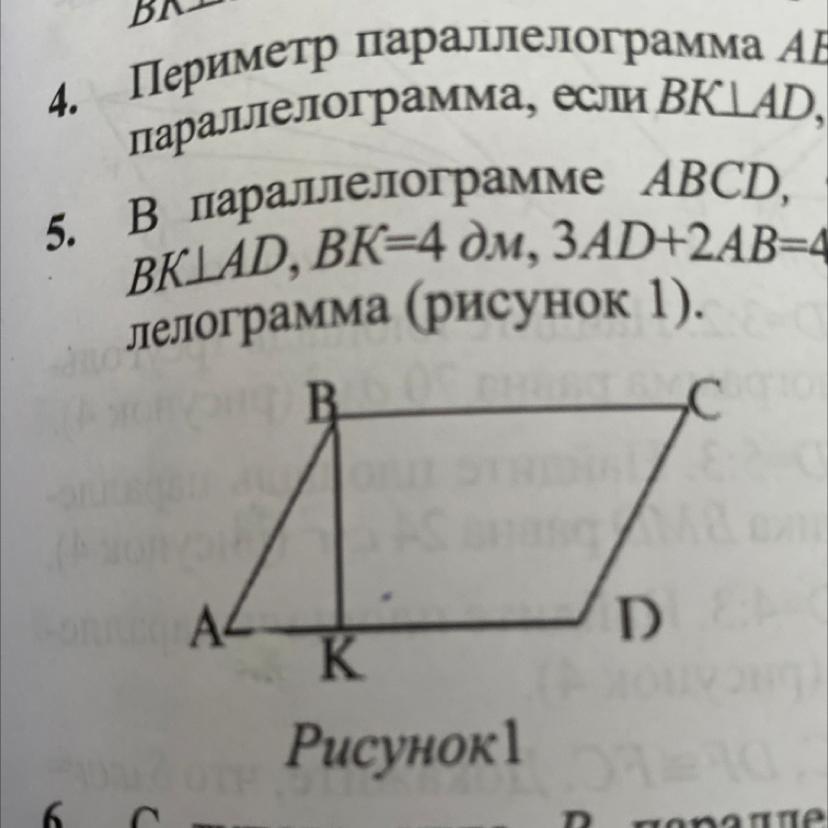
Периметр параллелограмма ABCD равен 80 дм .найдите площадь параллелограмма если BK высота AD ,угол A=30° ,AD-AB=12 дм ( рисунок 1)

Answer 1

Ответ:

Площадь параллелограмма равна 182 дм².

Объяснение:

Периметр параллелограмма ABCD равен 80 дм .Найдите площадь параллелограмма, если BK ⊥ AD , ∠A=30°, AD - AB = 12 дм.

Дано: ABCD - параллелограмм;

Р (ABCD) = 80 дм;

ВК - высота;

AD - AB = 12 дм;

∠А = 30°.

Найти: S(ABCD)

Решение:

• Площадь параллелограмма равны произведению основания на высоту, проведенную к данной стороне.

S = AD · BK

AD - AB = 12 дм (условие)

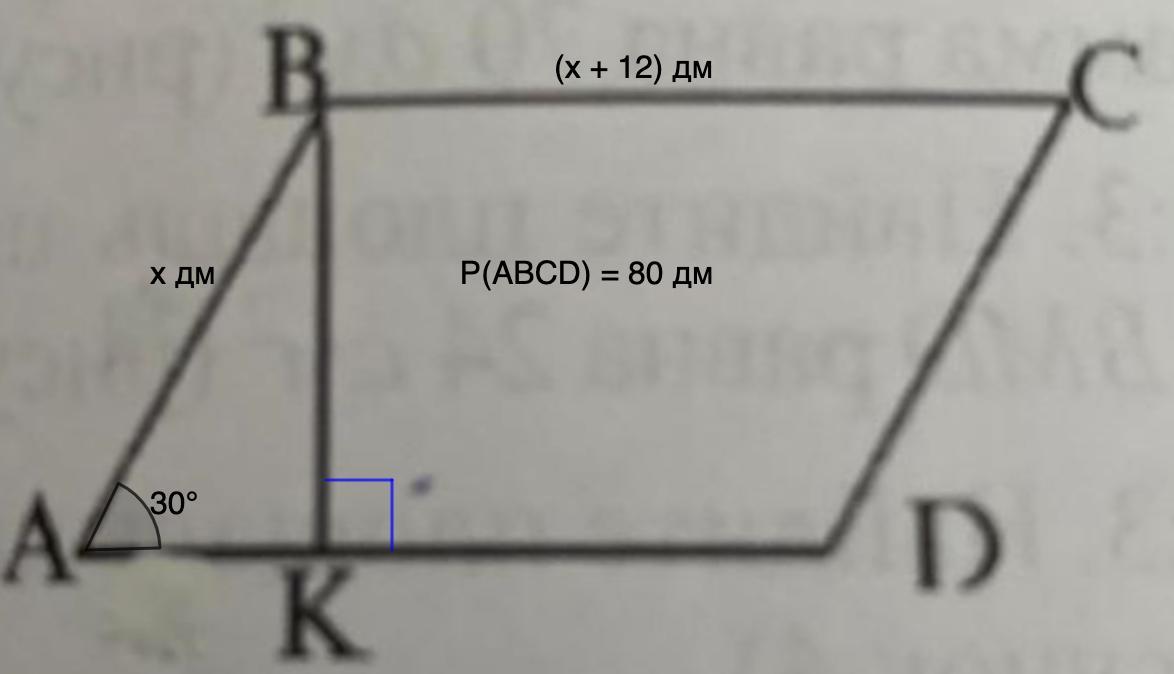
Пусть АВ = х дм, тогда AD = (x + 12) дм.

• Периметр параллелограмма равен удвоенной сумме смежных сторон.

P (ABCD) = 2 (AD + AB)

или

80 = 2(х + 12 + х)

4х + 24 = 80

4х = 56     |:4

x = 14

⇒ AB = 14 дм; AD = 26 дм.

Найдем высоту.

Рассмотрим ΔАВК - прямоугольный.

∠А = 30°

• Катет, лежащий против угла в 30°, равен половине гипотенузы.

⇒ ВК = АВ : 2 = 14 : 2 = 7 (дм)

Теперь можем найти площадь:

S(ABCD) = 26 · 7 = 182 (дм²)

#SPJ1