Даю 100 баллов геометрия

Ответы
Объяснение:
ЗАДАЧА №1
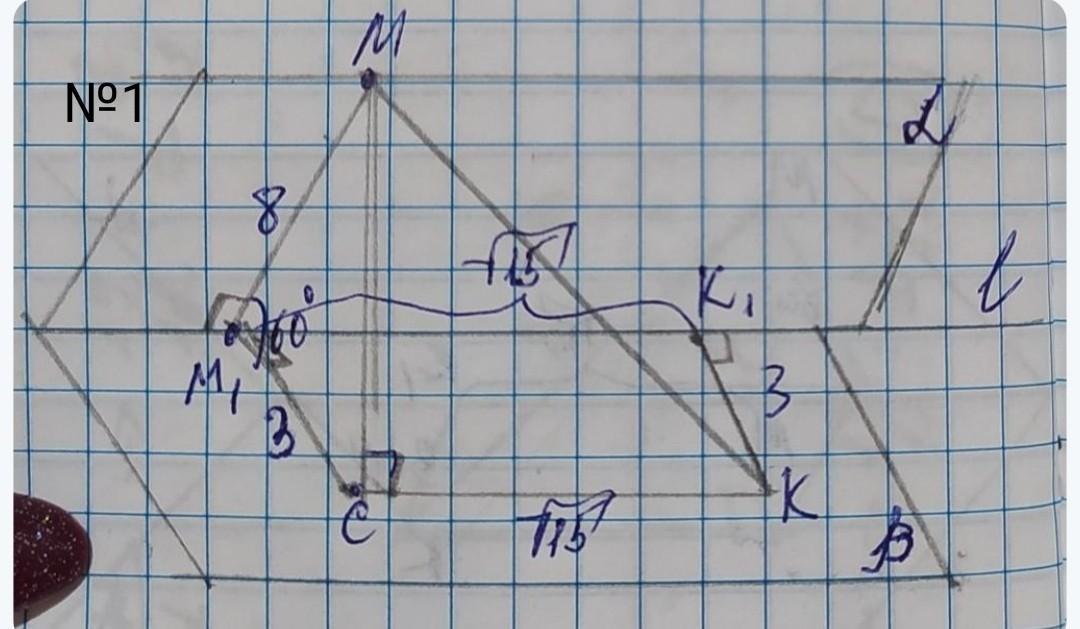
Угол между плоскостями α и β, пересекающимися по прямой L, равен 60°. В плоскостях α и β выбраны точки М и К соответственно из них проведены перпендикуляры ММ₁ и КК₁ к прямой L. КК₁=3см; ММ₁=8см; К₁М₁=√15см
Найдите длину отрезка МК
РЕШЕНИЕ:
Проведём от точки М₁ отрезок М₁С параллельный КК₁ и равный 3см, получился линейный ∠ММ₁С=60° . Из точки М проведём отрезок МС ⏊ β. Получили прямоугольный треугольник ММ₁С с прямым углом МСМ₁. Найдём МС по теореме косинусов:
МС²=ММ₁²+СМ₁²–2•ММ₁•СМ₁•cos60°=
=8²+3²–2•8•3•1/2=64+9–24=49
MC=√49=7(см).
∆МКС – прямоугольный, с прямым углом МСК.
По теореме Пифагора;
МК²=МС²+СК²=7²+(√15)²=49+15=64
МК=√64=8(см)
ОТВЕТ: МК=8см
ЗАДАЧА №2
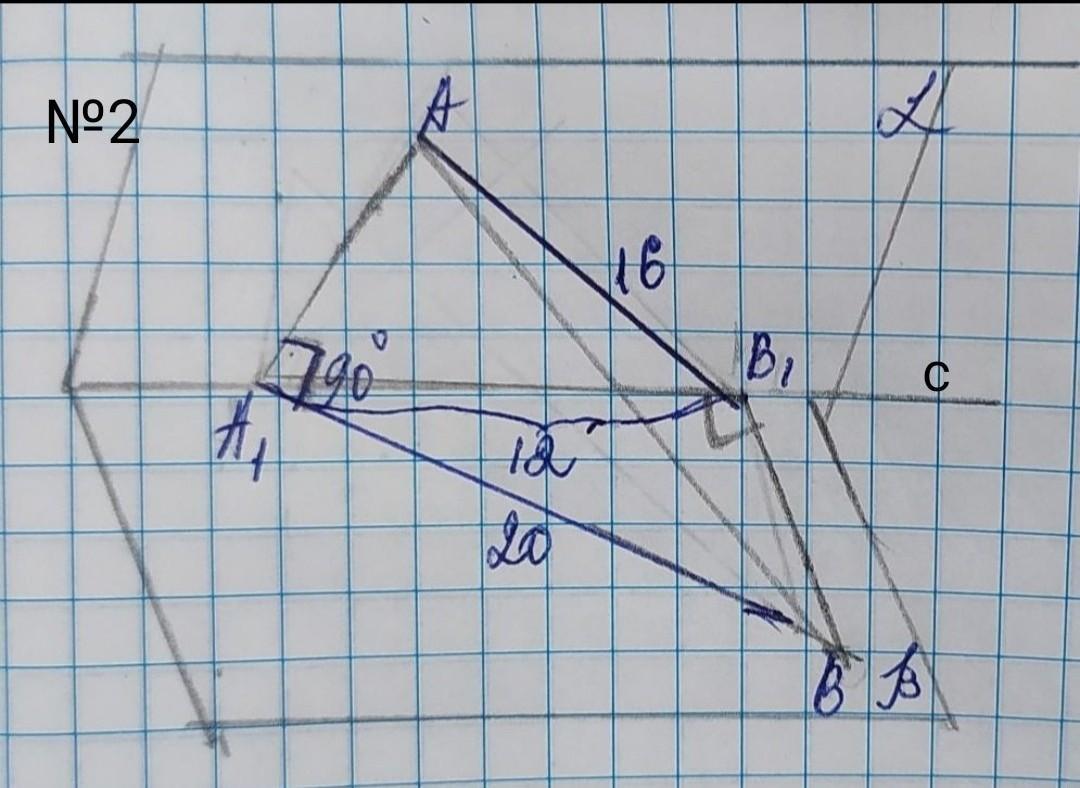
Концы отрезка лежат в двух перпендикулярных плоскостях. Проекции отрезков на плоскости равны 20 см и 16 см. Расстояние между основаниями перпендикуляров, проведённых из концов отрезков к линии пересечения плоскостей равно 12 см. Найти длину отрезка.
ДАНО:
плоскости α и β пересекаются по прямой с ; т.А ∈ α; т.В ∈ β; АА₁⏊ с; ВВ₁⏊ с; проекция А₁В=20 см; проекция АВ₁=16см; А₁В₁=12см
НАЙТИ: АВ
РЕШЕНИЕ:
ЕСЛИ ПЛОСКОСТИ ПЕРПЕНДИКУЛЯРНЫ, ТО ВСЕ ПРЯМЫЕ ЭТИХ ПЛОСКОСТЕЙ ПЕРПЕНДИКУЛЯРНЫ МЕЖДУ СОБОЙ, поэтому АА₁⏊А₁В и АВ₁⏊ВВ₁.
∆А₁В₁В – прямоугольный с прямым углом А₁В₁В.
По теореме Пифагора:
А₁В²=А₁В₁²+ВВ₁² → ВВ₁²=А₁В²–А₁В₁²=
20²–12²=400–144=256
ВВ₁=√256=16(см)
∆АВ₁В – прямоугольный, равнобедренный с прямым углом АВ₁В. В равнобедренном прямоугольном треугольнике гипотенуза больше катета в √2 раз, поэтому АВ=16•√2=16√2(см).
Или по теореме Пифагора:
АВ²=АВ₁²+ВВ₁²=16²+16²=256+256=512
АВ=√512=√(256•2)=16√2(см)
ОТВЕТ: АВ=16√2 см