Question

Даю 100 баллов геометрия​

Answer 1

Объяснение:

ЗАДАЧА №1

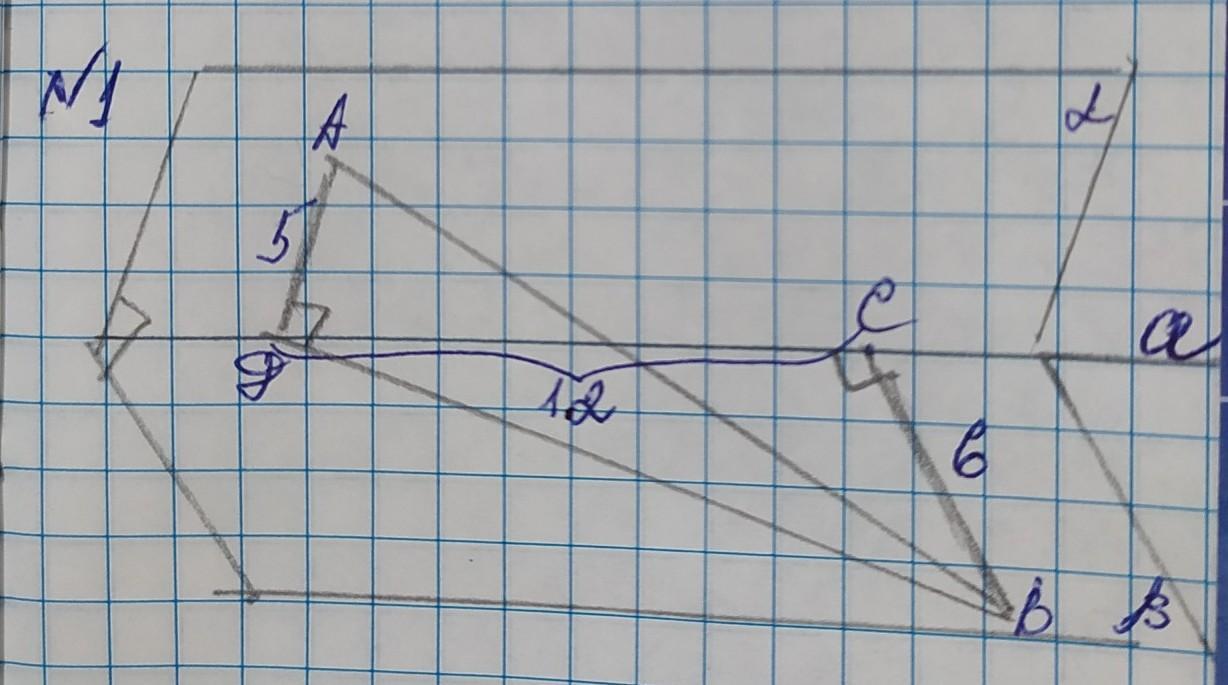
Точки А и В принадлежат двум перпендикулярным плоскостям α и β соответственно, а – линия пересечения этих плоскостей, АД и ВС – перпендикуляры, проведенные из точек А и В к прямой а. АД=5см; ВС=6см; ДС=12см

Найти длину отрезка АВ

РЕШЕНИЕ:

ЕСЛИ ПЛОСКОСТИ ПЕРПЕНДИКУЛЯРНЫ, ТО ЛЮБАЯ ПРЯМАЯ ОДНОЙ ПЛОСКОСТИ БУДЕТ ПЕРПЕНДИКУЛЯРНА ЛЮБОЙ ПРЯМОЙ ВТОРОЙ ПЛОСКОСТИ, поэтому АД⏊ВД.

∆ВДС – прямоугольный, с прямым углом С. По теореме Пифагора:

ВД²=СД²+ВС²=12²+6²=144+36=180

ВД=√180=6√5(см).

∆АВД – прямоугольный с прямым углом АДВ.

По теореме Пифагора:

АВ²=АД²+ВД²=5²+(√180)²=25+180=205

АВ=√205(см)

ОТВЕТ: АВ=√205 см

ЗАДАЧА №2

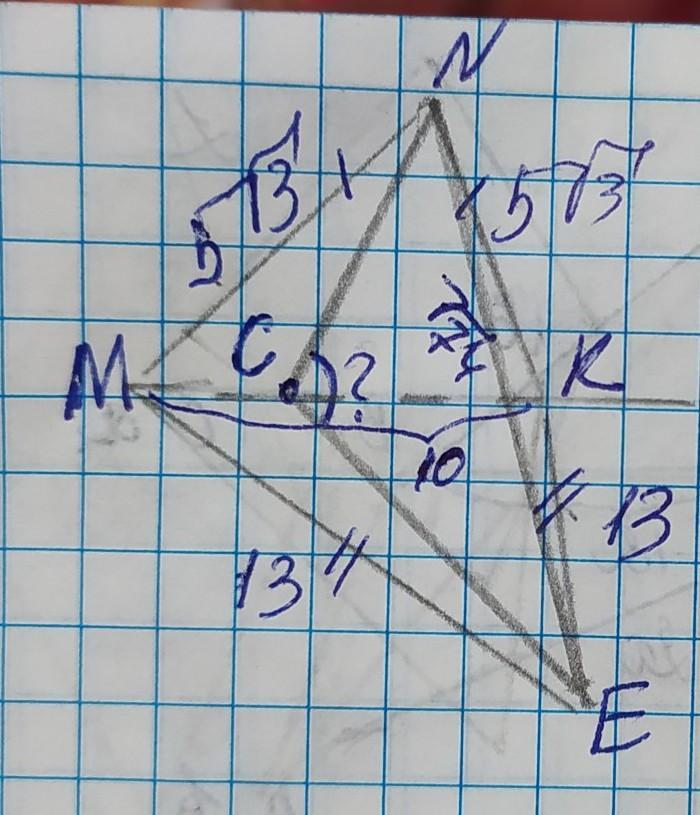
Два равнобедренных треугольника MNK и MEK имеют общее основание МК. MN=5√3 см; ЕК=13см; ЕN=√74см; МК=10см.

Найти угол между плоскостями MNK и МЕК

РЕШЕНИЕ:

проведём от точки N и от точки Е перпендикуляры к основанию МК, пусть их общей точкой пересечения будет точка С, ∠NСЕ – линейный угол, который нужно найти.

Так как треугольники МNK и MEK равнобедренные, то их боковые стороны равны, поэтому MN=NК=5√3см и МЕ=ЕК=13см.

В равнобедренном треугольнике высота, проведённая к основанию является ещё медианой, которая делит основание МК пополам, поэтому

МС=СК=10÷2=5(см)

∆МNС – прямоугольный с катетами NС и МС и гипотенузой МN.

По теореме Пифагора:

NМ²=NС²+МС² → NС=NМ²–МС²=(5√3)²–5²=

=25•3–25=75–25=50

NС=√50=5√2(см)

В ∆МЕК высота ЕС также является медианой, и делит ∆МЕК на 2 равных прямоугольных треугольника МЕС и КЕС.

Из ∆МЕС по теореме Пифагора:

МЕ²=ЕС²+МС² → ЕС²=МЕ²–МС²=13²–5²=169–25=

=144

ЕС=√144=12(см).

Рассмотрим ∆NСЕ. Используя теорему косинусов:

$\\ \cos(nce) = \frac{nc {}^{2} + ec {}^{2} - ne {}^{2} }{2 \times nc \times ec} = \\ \\ = \frac{( \sqrt{50} ) {}^{2} + 12 {}^{2} - ( \sqrt{74} ) {}^{2} }{2 \times \sqrt{50} \times 12} = \\ \\ = \frac{50 + 144 - 74}{24 \sqrt{50} } = \frac{120}{24 \times 5 \sqrt{2} } = \\ \\ = \frac{120}{120 \sqrt{2} } = \frac{1}{ \sqrt{2} } = \frac{1 \times \sqrt{2} }{ \sqrt{2 \times \sqrt{2} } } = \\ \\ \frac{ \sqrt{2} }{2}$

cosNCE=√2/2 → ∠NCE=45°

ОТВЕТ: ∠NCE=45°