Предмет: Геометрия,
автор: abramov1998
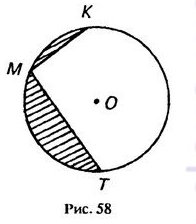
На рисунке 58 хорды МК и МТ стягивают дуги в 60° и 120°. Радиус окружности равен R. Найдите площадь заштрихованной фигуры.
Приложения:
Ответы
Автор ответа:
0
Проводим КТ, дуга КТ=360-дуга МК-дуга МТ=360-60-120=180, КТ-диаметр, уголМ=90-вписанный угол , опирается на диаметр=1/2дугиКТ=180/2=90, треугольник МКТ прямоугольный, КТ=R+R=2R, проводим радиус МО=R треугольник МОТ равнобедренный, МО=ОТ=R, уголМОТ-центральный=дуге МТ=120, уголОТМ=уголОМТ=(180-120)/2=30, МК=1/2КТ=2R/2=R, МТ=КТ*cos30=2R*корень3/2=R*корень3, площадь МКТ=1/2*МК*МТ=1/2*R*R*корень3=R в квадрате*корень3/2, площадь 1/2 окружности=пи*R в квадрате/2, площадь заштрихованной=площадь полукруга-площадьМКТ=(пи*R в квадрате/2) - (R в квадрате*корень3/2)=(R в квадрате/2) * (пи-корень3)
Похожие вопросы
Предмет: Қазақ тiлi,
автор: nazerke0536
Предмет: Литература,
автор: Аноним
Предмет: Химия,
автор: iruk0909
Предмет: История,
автор: Мерш