Предмет: Алгебра,
автор: iiinnnnnaa
70 баллов
разрешите неравенство
Приложения:
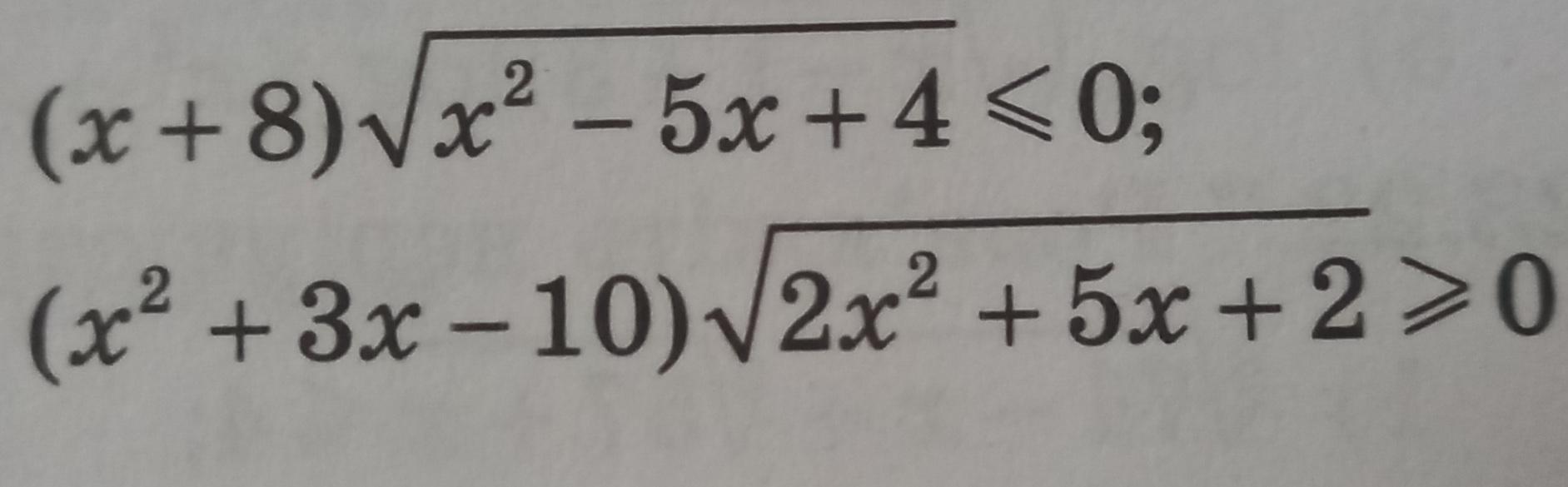

Ответы
Автор ответа:
1
Ответ: 1) x∈ (-∞;-8] 2)х∈(-∞;-5]U[2;+∞)
Объяснение:
Найдем ОДЗ
Выражение под корнем должно быть неотрицательным
По т. Виета х1=1; х2=4 => ОДЗ: x∈(-∞; 1]U[4;+∞)
Заметим, что выражение для всех х из ОДЗ
Тогда вся левая часть неравенства будет меньше или равна 0 , если х+8≤ 0 => x≤-8
=> x∈ (-∞;-8] . Все значения х из этого интервала принадлежат ОДЗ
Значит решение неравенства x∈ (-∞;-8]
2).
ОДЗ 2х²+5х+2 =0
х1=-2 ; x2 =-0.5
=> ОДЗ : x∈ (-∞;-2]U[-0.5;+∞)
Заметим, что выражение для всех х из ОДЗ
Тогда вся левая часть неравенства будет больше или равна 0 , если х²+3х-10 ≥0
х²+3х-10 =0
х1=-5 х2=2
х∈(-∞;-5]U[2;+∞) . Все указанные решения входят в ОДЗ
=> Ответ х∈(-∞;-5]U[2;+∞)
Похожие вопросы
Предмет: Алгебра,
автор: beautifulme
Предмет: Физика,
автор: Изумрудная000Звезда
Предмет: Алгебра,
автор: kseniashepelevaabc
Предмет: Математика,
автор: kasancukdianka