Question

Пошлите решить пожалуйста

Answer 1

Ответ:

Диагонали прямоугольника равны 24 см.

Объяснение:

Найти диагонали прямоугольника.

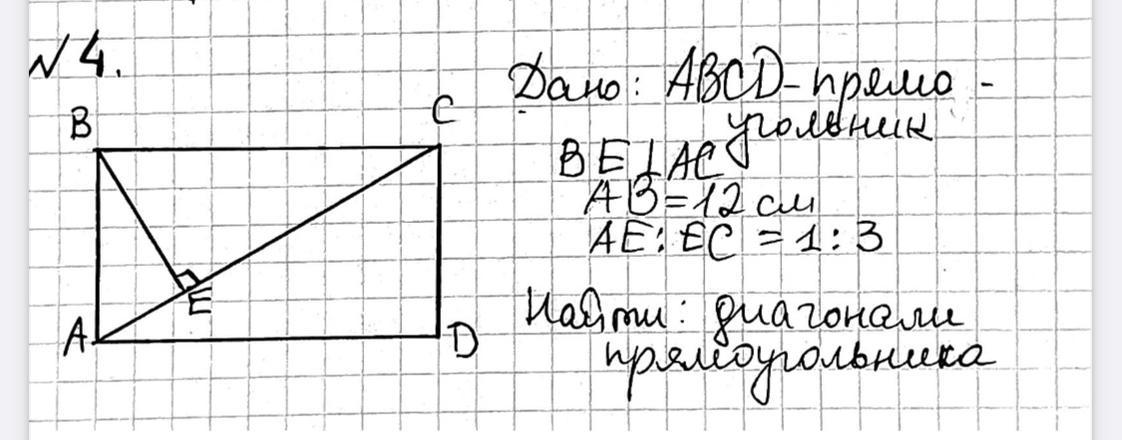
Дано: ABCD - прямоугольник;

ВЕ ⊥ АС; АВ = 12 см;

АЕ : ЕС = 1 : 3

Найти: АС.
Решение:

АЕ : ЕС = 1 : 3

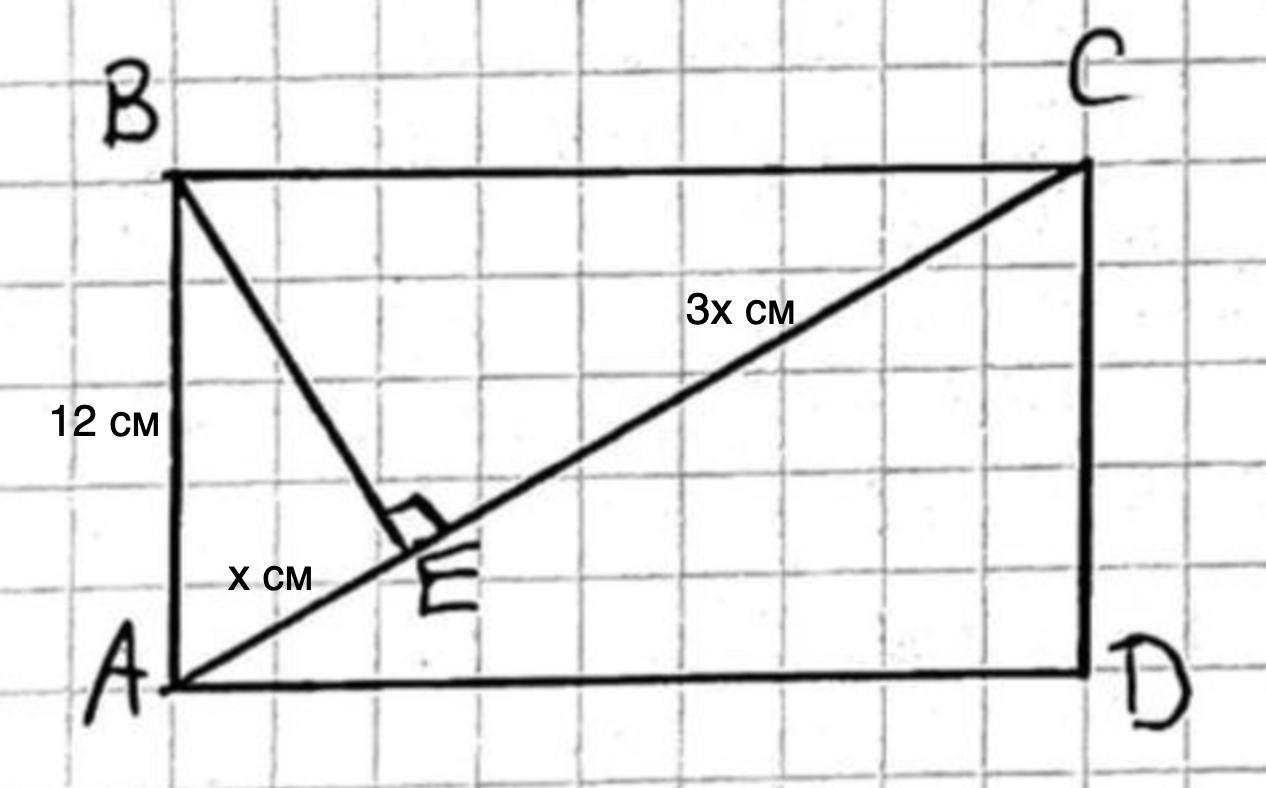
Пусть АЕ = х см, тогда ЕС = 3х см, а АС = 4х см.

Рассмотрим ΔАВС - прямоугольный.

Метрические соотношения в прямоугольном треугольнике:

• Квадрат катета равен произведению гипотенузы и проекции этого катета на гипотенузу.

⇒ АВ² = АЕ · АС

144 = х · 4х

4х² = 144

х² = 36

х = ±6

Отрицательный корень не подходит по условию задачи.

⇒ АС = 4х = 6 · 4 = 24 (см)

• В прямоугольнике диагонали равны.

Диагонали прямоугольника равны 24 см.