Знайти площі заштрихованих фігур.
Даю 100 балов!
Написать полное решение плиз
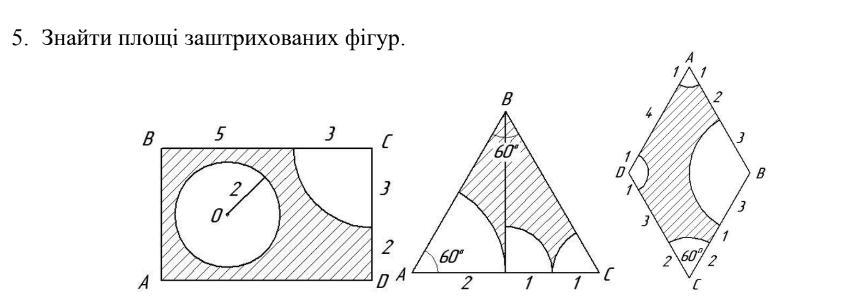
Ответы
Фігура №1:
1) Знайдемо загальну площу прямокутника ABCD:
S = BC * CD
S = (5 + 3) * (3 + 2) = 40 (см²)
2) Знайдемо площу круга радіус якого дорівнює 2 см за формулою:
S = 3,14 * 2² = 12,56 (см²)
3) Знайдемо площу сектора який розташований в правому верхньому кутку прямокутника з радіусом 3 см за формулою:
S = 7,065 (см²)
4) А тепер, від загальної площі прямокутника віднімемо площу круга та площу сектора, запишемо:
S = 40 - 12,56 - 7,065 = 20,375 (см²)
Відповідь: на першій фігурі заштрихована площа складає 20,375 см²
Фігура №2:
1) Розглянемо трикутник, в ньому перший і другий кут дорівнює 60°, тоді третій кут дорівнюватиме 180° - 60° - 60° = 60°
Тобто, цей трикутник є рівностороннім трикутником у якого всі сторони рівні між собою. AC = CB = BA
AC = 2 + 1 + 1 = 4 (см)
2) Для початку, знайдемо загальну площу трикутника, для цього скористаємося формулою для знаходження площі рівностороннього трикутника:
(см²)
3) Знайдемо площу першого сектора, кут якого дорівнює 60°, а радіус 2 см. Тобто сектор від кута А, за формулою:
S = 2,093 (см²)
4) Розглянемо трикутник ABC знову, як можна спостерігати в нас від точки B йде бісектриса, а бісектриса в рівносторонньому трикутнику завжди є і медіаною і висотою. Тоді, знайдемо площу другого сектора, кут якого дорівнює 90°, а радіус 1 см.
S = 0,785 (см²)
5) Знайдемо площу третього сектора, кут якого дорівнює 60°, а радіус 1 см. Тобто сектор від кута С:
S = 0,523 (см²)
6) А тепер, від загальної площі трикутника віднімемо площу першого, другого та третього сектора, запишемо:
S = 4√3 - 2,093 - 0,785 - 0,523 ≈ 3,527 (см²)
Відповідь: на другій фігурі заштрихована площа складає 3,527 см²
Фігура №3:
1) Розглянемо фігуру, як можна спостерігати це ромб, тому що в в ньому всі сторони між собою рівні.
2) Для початку знайдемо одну зі сторін ромба, наприклад сторону AC: 1 + 4 + 1 = 6 (см)
3) Тепер знайдемо загальну площу ромба ABCD за формулою:
S = a² * sin(α)
S = 6² * sin(60°) = 36 * √3 / 2 =
Знайдемо площі секторів кутів A, B, C, D за формулою:
3) Знайдемо площу сектора від кута A (протилежні кути у паралелограма рівні, тому ∠С = ∠А) радіус якого дорівнює 1 см =
S = 0,523 (см²)
4) Знайдемо площу сектора від кута B, але для початку знайдемо ∠B = 180° - 60° = 120°
Радіус сектора дорівнює 3 см, тому площа:
S = 9,42 (см²)
5) Знайдемо площу сектора від кута C радіус сектора дорівнює 2 см:
S = 2,093 (см²)
6) Знайдемо площу сектора від кута D радіус сектора дорівнює 1 см:
S = 1,047 (см²)
7) А тепер, від загальної площі ромба віднімемо площу першого, другого, третього та четвертого сектора, запишемо:
S = = - 0,523 - 9,42 - 2,093 - 1,047 ≈ 18,094 (см²)
Відповідь: на третій фігурі заштрихована площа складає 18,094 (см²)