Предмет: Математика,
автор: kotorakta45
Обчислить подвійний інтеграл по області Д, обмеженої вказаними лініями.
Приложения:
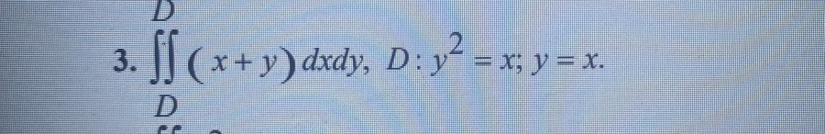
Ответы
Автор ответа:
0
Ответ:
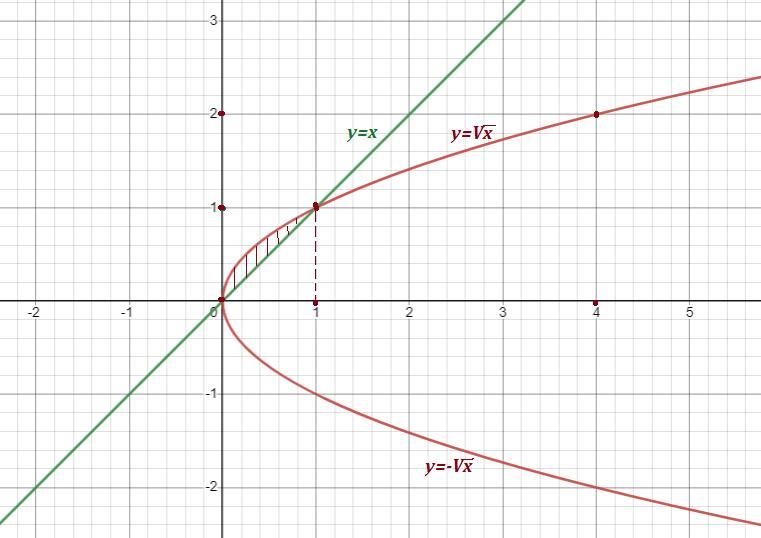
Вычислить двойной интеграл по области D .
,
.
Точки пересечения:
.
Приложения:
Похожие вопросы
Предмет: Химия,
автор: Olyakvit
Предмет: Математика,
автор: Trotskovets
Предмет: Алгебра,
автор: Аноним
Предмет: Математика,
автор: sofiaanapiaeva
Предмет: Математика,
автор: asymalieva