Question

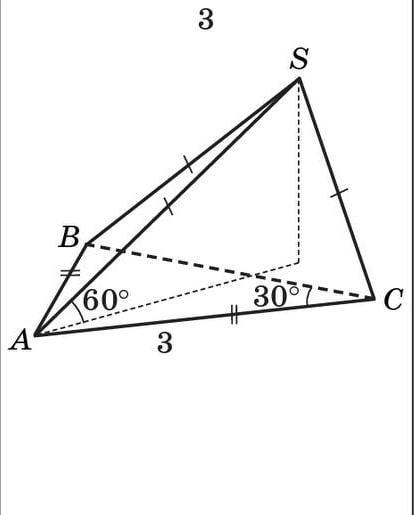
Найти объем. SO - высота
Знайти об'єм. SO - висота

Answer 1

Ответ:

$\dfrac{27}{4}.$

Пошаговое объяснение:

По условию в основании лежит равнобедренный треугольник CAB с углом при основании в $30^{\circ}.$ Чтобы найти площадь основания, опустим высоту AD на сторону BC (она же биссектриса и медиана в силу равнобедренности). Из прямоугольного треугольника ACD находим

$AD=AC\cdot \sin 30^{\circ}=\dfrac{3}{2};\ DC=AC\cdot \cos 30^{\circ}=\dfrac{3\sqrt{3}}{2};\ BC=2DC=3\sqrt{3};$

                            $S_{ABC}=\dfrac{1}{2}AD\cdot BC=\dfrac{9\sqrt{3}}{4}.$

Далее, поскольку по условию AS=BS=CS, ттреугольники ASO, BSO и CSO равны (они прямоугольные с равными гипотенузами и общим катетом SO). Поэтому AO=BO=CO, то есть O - центр окружности, описанной вокруг треугольника ABC. Как известно, ее радиус вычисляется по формуле

                                     $R=\dfrac{AB\cdot BC\cdot CA}{4S_{ABC}}=3.$

Кстати, ответ можно было предсказать, если заметить, что наш треугольник является частью правильного шестиугольника со стороной 3.

Итак, AO=R=3, а тогда из прямоугольного треугольника ASO  с острым углом A в 60 градусов, находим

                                     $SO=AO\cdot {\rm tg}\ 60^{\circ}=3\sqrt{3}.$

Остается найти объем пирамиды по формуле

                          $V=\dfrac{1}{3}S_{ABC}\cdot SO=\dfrac{1}{3}\cdot \dfrac{9\sqrt{3}}{4}\cdot 3\sqrt{3}=\dfrac{27}{4}.$