Question

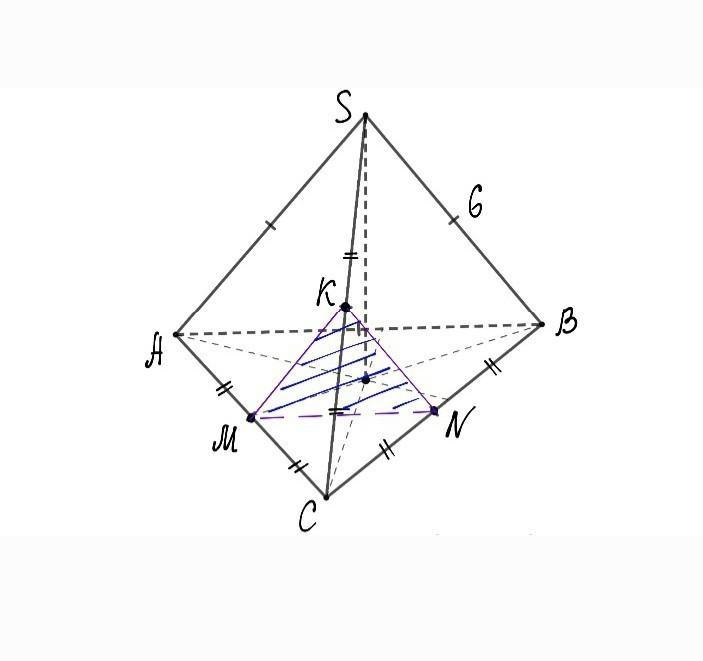
Постройте сечение треугольной пирамиды SABC плоскостью, проходящей через точку N - середину ребра ВС и параллельной плоскости SAB. Найдите периметр полученного сечення, если каждое ребро пирамиды имсет длину 6.

Answer 1

Ответ:

9

Объяснение:

Дано:

SABC - треугольная пирамида

Ребра равны 6

Построить:

Сечение , проходящей через N-середину ребра ВС и параллельной (SAB).

Найти: P.сечения

Решение:

Для того , чтобы плоскость сечения была параллельной (SAB) - то две пересекающие прямые, лежащие в каждой из плоскостей , - должны быть параллельны .Так как т.N - середина ВС ,то вспомним:

• Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника. 

Таким образом мы можем сделать вывод , что плоскость сечения пересекает плоскости - (АSC) , (BSC) , (ACB) по средним линиям и параллельна (SAB) , пусть искомым сечением будет ∆MKN.

По условию все ребра пирамиды равны 6 . Так как среднии линии равны половине основания - то ∆MKN со сторонами , равными 3-ём . Треугольник MKN - равносторонний. Перриметр равностороннего треугольника найдем по формуле P = 3a , где a - сторона треугольника , то есть:

$P_{_{\vartriangle MKN}}=3a = 3\cdot 3=9$