Предмет: Алгебра,
автор: paulinasvetlana1
допоможіть обчисліть інтеграл
Приложения:
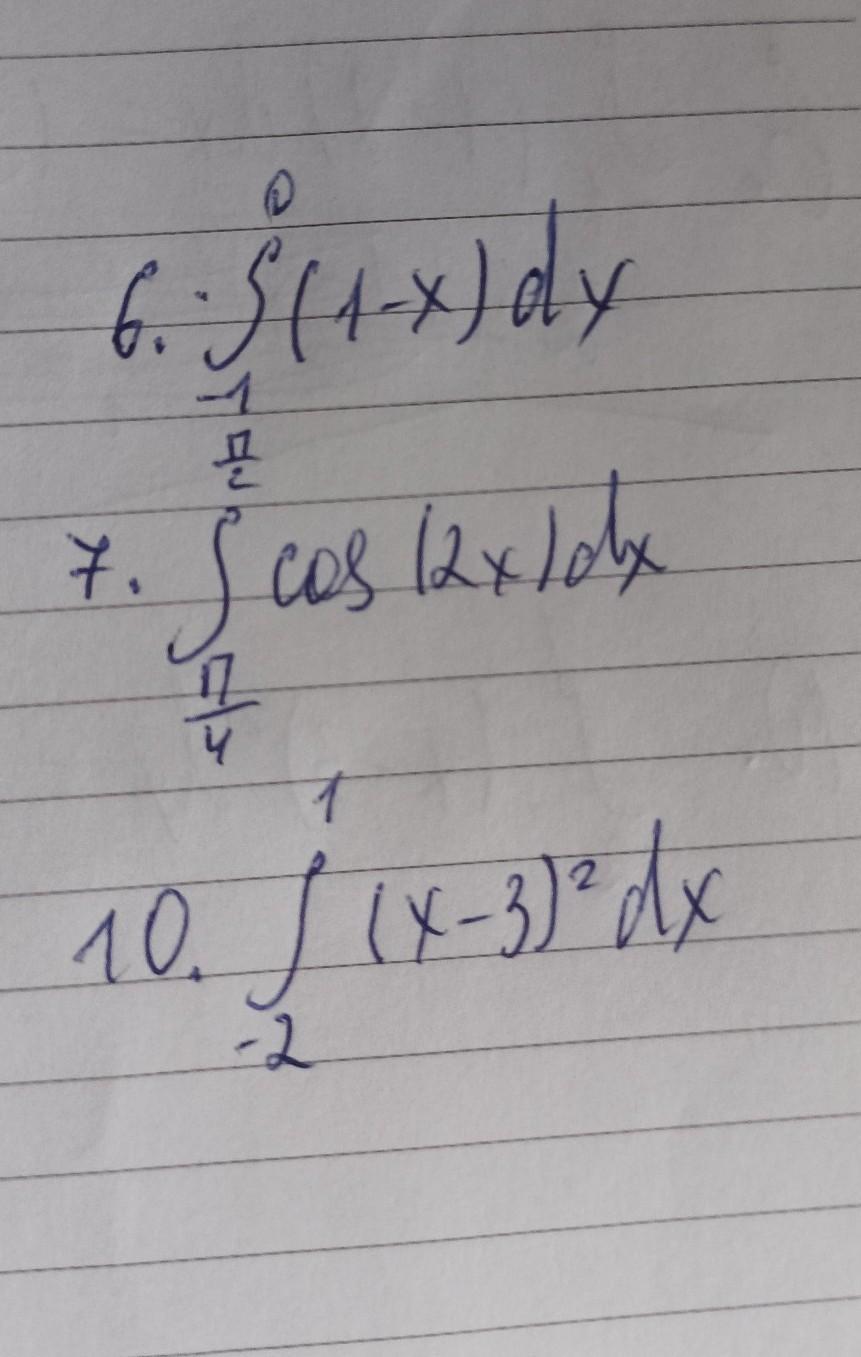
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Химия,
автор: karishoookkkkk
Предмет: Математика,
автор: ggulnarm
Предмет: Физика,
автор: levaoleksi5
Предмет: Английский язык,
автор: lemon12559