Question

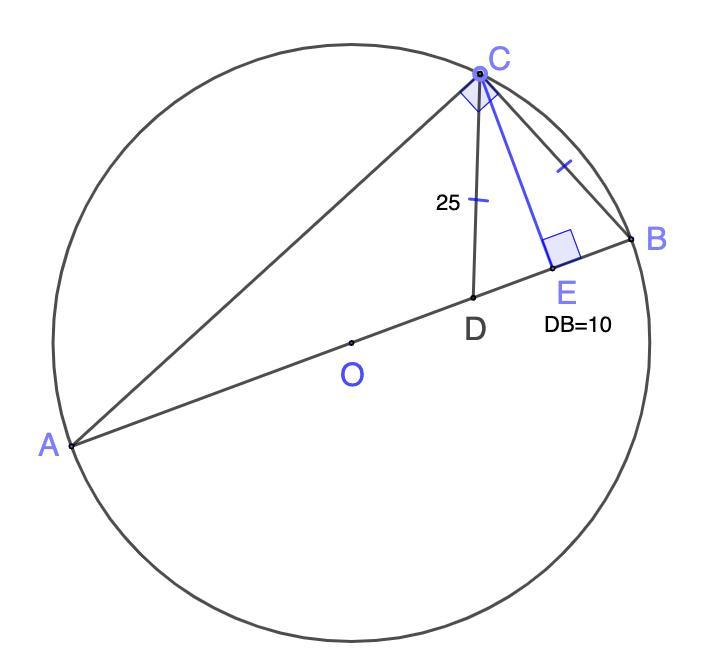
В окружности с центром О и диаметром АВ, на отрезке ОВ взяли точку D, а на дуге ВА взяли точку С, такую что |DC|=|CB|=25 и |DB|=10. Найдите длину отрезка АВ. D​

Answer 1

Ответ:

Диаметр АВ равен 125 ед.

Пошаговое объяснение:

В окружности с центром О и диаметром АВ, на отрезке ОВ взяли точку D, а на дуге ВА взяли точку С, такую что |DC|=|CB|=25 и |DB|=10. Найдите длину отрезка АВ.

Дано: Окр.(О);

АВ - диаметр;

D ∈ ОВ; С ∈ ◡АВ;

DC = CB = 25; DB = 10.

Найти: АВ.

Решение:

Проведем СЕ ⊥ АВ.

Рассмотрим ΔDCB - равнобедренный.

СЕ - высота.

• В равнобедренном треугольнике высота, проведенная к основанию, является медианой.

⇒ DE = EB = 10 : 2 = 5 (ед.)

Рассмотрим ΔАСВ.

• Вписанный угол, опирающийся на диаметр, равен 90°.

⇒ ΔАСВ - прямоугольный.

СЕ - высота.

• Метрические соотношения в прямоугольном треугольнике:
• Квадрат катета равен произведению гипотенузы и проекции этого катета на гипотенузу.

⇒ СВ² = ЕВ · АВ

625 = 5 · АВ

АВ = 125

Диаметр АВ равен 125 ед.

#SPJ1