Предмет: Алгебра,
автор: mitaki26052006
Помогите пожалуйста!!!! 20 балов
Приложения:
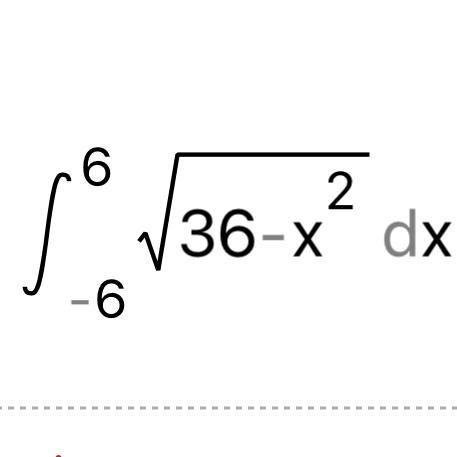
Ответы
Автор ответа:
2
Ответ:
Найдём сначала неопределённый интеграл, применяя тригонометрическую замену .
Теперь вычислим определённый интеграл, применяя формулу Ньютона-Лейбница .
lolayoulhhghh:
Добрый день помогите пожалуйста с историей если можете для меня очень важна эта робота, задание у меня в профиле.
Похожие вопросы
Предмет: Алгебра,
автор: 0932097859
Предмет: Алгебра,
автор: Аноним
Предмет: Алгебра,
автор: Аноним
Предмет: История,
автор: dzordonovagulnara
Предмет: Русский язык,
автор: lanskov1995