Помогите пожалуйста, как это решить?!
Ответы
Відповідь:
Примітка: Я не знаю в якій формі має бути відповідь, тому тут 2 варіанти і через π і без π. + малюнки схематичні.
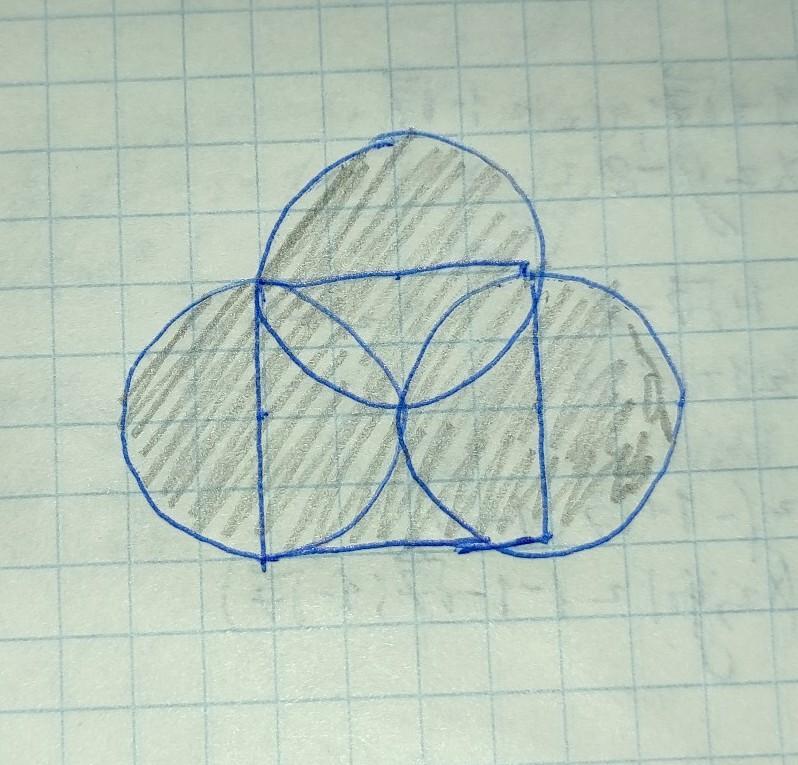
Завдання №1: (малюнок вгорі, він схематичний, оскільки в мене немає циркуля).
Заштрихована область це 4 кола які перетинаються
Області їх перетину можна окреслити квадратом, тоді все, що залишиться знайти це площу внутрішнього квадрата і чотирьох півкіл( 2 цілих кола).
1) Знайдемо площу квадрата зі стороною 4 см( 1 клітинка має сторону довжиною в 1 сантиметр.)
Sкв. = a², де a – сторона квадрата, a = 4 см.
Sкв. = 4² = 16(см²)
2) Тепер знайдемо площу 4 півкіл,які уявно складають 2 цілих кола:
Sобл. = 4πr²/2 = 2πr² .
Sобл. = 2π·2² = 8π ≈ 25,13(см²)
3) S = Sкв.+ Sобл.
S = 16+8π = 8(2+π) ≈ 41,13(см²)
Відповідь: 8(2+π)см² або 41,13 см².
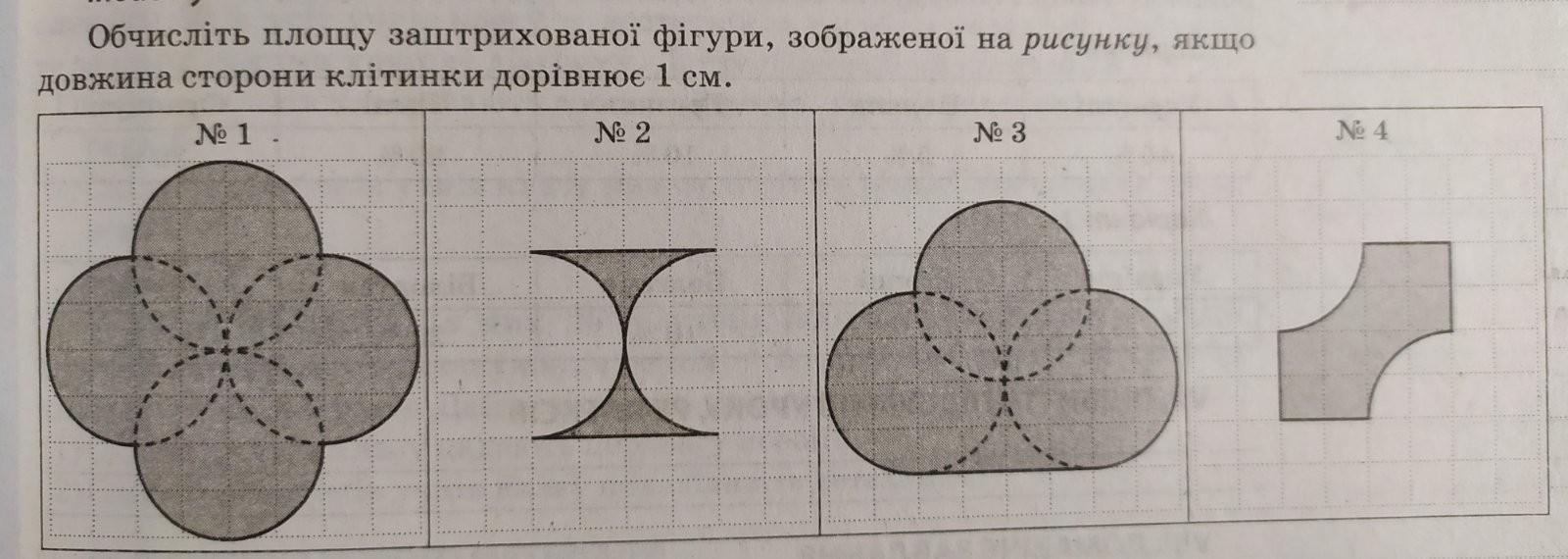
Завдання №2:
Маємо квадрат з якого вирізали дві половини кола, тобто ми повинні знайти площу квадрата та площу вирізаної області (двох півкіл) і відняти від площі квадрата площу кола):
a – сторона квадрата,
Sкв. = a², де a = 4 см (Оскільки довжина сторони клітинки 1 см)
Sкв. = 4² = 16 (см²)
Тепер знайдемо площу кола радіусом 2 см:
Sк. = πr²
Sк. = π·2² = 4π ≈ 4·3,14 = 12,56
Знайдемо площу заштрихованої фігури:
S = Sкв.-Sк.
S = 16-4π = 4(4-π) ≈ 3,43(см²)
Відповідь: (16-4π) см² або 3,43 см²
Завдання №3:
У даному випадку ми можемо накреслити квадрат в центрі фігури(на фото вгорі), тоді це, що нам залишається це знайти площу цього квадрата та трьох півкіл, а потім їх суму.
1) Sкв. = a², де a = 4 см
Sкв. = 4² = 16(см²)
2) Тепер знайдемо площу трьох півкіл:
Sобл. = 3Sк/2 = 3·πr²/2.
Sобл. = 3·π·2²/2 = 6π(см²)
3) Знайдемо площу заштрихованої фігури:
S = Sкв. + Sобл.
S = 16+6π = 2(8+3π) ≈ 34,85(см²)
Відповідь: 2(8+3π) см² або 34,85 см².
Завдання №4:
Ця фігура це квадрат зі стороною 4 см, з якого вирізали 2 четверті(тобто половину) кола радіусом 2 см:
Знайдемо площу квадрата:
Sкв. = a², a = 4 см
Sкв. = 4² = 16(см²)
Площа півкола: Sп.к. = (πr²)/2
Sп.к. = (π·2²)/2 = 4π/2 = 2π ≈ 3,14·2 = 6,28(см²)
Тепер знайдемо площу заштрихованої фігури:
S = Sкв. - Sп.к
S = 16-2π = 2(8-π) ≈ 9,72(см²)
Відповідь:2(8-π)см² або 9,72 см².