Предмет: Геометрия,
автор: gamanuk79
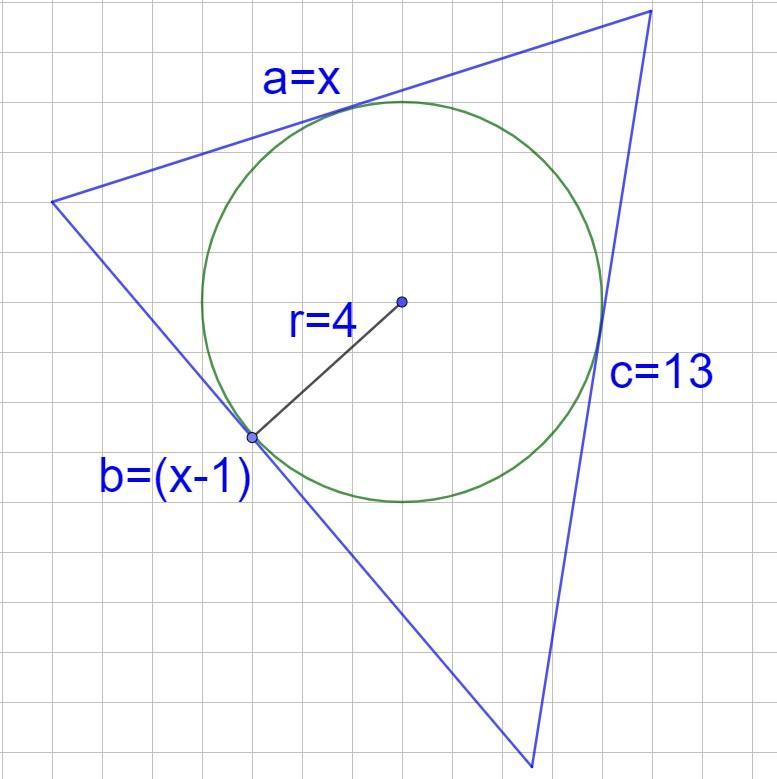
У трикутнику одна зі сторін дорівнює 13 см, а різниця двох інших – 1 см. Знайдіть ці дві сторони, якщо радіус кола, вписаного в трикутник, дорівнює 4 см.
Ответы
Автор ответа:
5
Ответ:
14 cм, 15 см
Объяснение:
У трикутнику одна зі сторін дорівнює 13 см, а різниця двох інших – 1 см. Знайдіть ці дві сторони, якщо радіус кола, вписаного в трикутник, дорівнює 4 см.
Радіус r вписаного кола можна обчислити за формулами:
де р - півпериметр трикутника, S – його площа.
За формулою Герона площа трикутника:
де a, b, c – довжини сторін трикутника. Тоді:
Позначимо першу невідому сторону трикутника a за х см, тоді друга сторона b буде дрорівнювати (х-1) см. За умовою третя сторона c трикутника дорівнює 13 см, тоді півпериметр трикутника:
(см)
Радіус кола, вписаного в трикутник, дорівнює 4 см. Складаємо рівняння:
42(x-7)=16(x+6)
42x-294=16x+96
26x=390
x=15
Маємо: а=15 (см), b=15-1=14 (см)
Відповідь: 14 cм, 15 см
#SPJ1
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: juliasmurova14
Предмет: Информатика,
автор: katya35527
Предмет: Математика,
автор: emyreshko
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: 89018706253alina