Предмет: Геометрия,
автор: mskdkdkwk83838
100 баллов!!!
В правильной пирамиде SABCD боковое ребро, равное 6 образует с основанием 60 градусов. Вычислите угол между боковой гранью основанием пирамиды.
Помогите пожалуйста, и если можно, то с рисунком, умоляю
Ответы
Автор ответа:
2
Ответ:
≅ 72°
Объяснение:
1) Найдём высоту SO через синус. sin 60° = SO/SC, откуда SO = SC * sin 60°. SO =
2) Проведём апофему SK. Далее для нахождения SK, найдём OC с теоремы Пифагора. И так, имеем следующее:
3) Найдём сторону AC
AC = 2 * OC
AC = 2 * 3 = 6
4) Так как пирамида у нас правильная, то основанием является квадрат. Найдём сторону квадрата через диагональ AC.
это сторона квадрата
5) Найдём отрезок OK.
OK = BC / 2
6) За тангенсом найдём угол OKS.
За таблицей тангенсов находим соответствующий приближенный градус tg 3 ≅ 72°
Приложения:
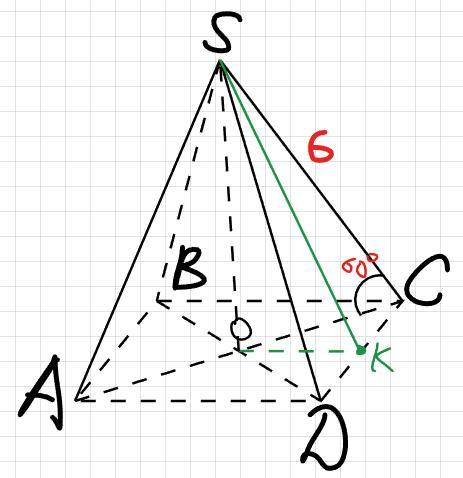
mskdkdkwk83838:
спасибо большое
Похожие вопросы
Предмет: Литература,
автор: bdbdhdshsjzj
Предмет: Алгебра,
автор: 1224872
Предмет: Математика,
автор: Gemasik
Предмет: Биология,
автор: sinmerti