Question

У відповідь записати найменший цілий розв'язок нерівності на проміжку[0;2π].​

Answer 1

Ответ:

Неравенство   $\bf \sqrt3\, sinx+cosx < 1$  .

Метод вспомогательного угла .  $\bf (\sqrt3)^2+1^2=3+1=4$   ⇒   делим

уравнение на $\bf \sqrt4=2$  .

$\bf \dfrac{\sqrt3}{2}\, sinx+\dfrac{1}{2}\, cosx < \dfrac{1}{2}\\\\cos\dfrac{\pi}{6}\, sinx+sin\dfrac{\pi}{6}\, cosx < \dfrac{1}{2}\\\\sin(x+\dfrac{\pi }{6}) < \dfrac{1}{2}$

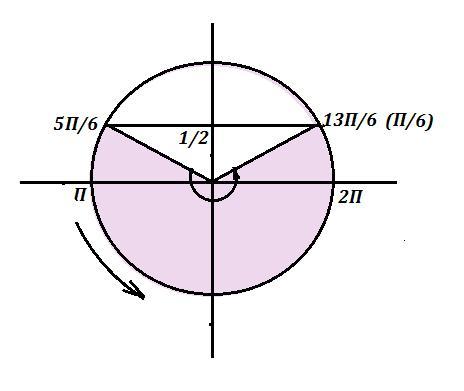
Смотри рисунок .

$\bf \dfrac{5\pi }{6}+2\pi n < x+\dfrac{\pi }{6} < \dfrac{13\pi }{6}+2\pi n\ \ ,\ n\in Z\\\\\dfrac{4\pi }{6}+2\pi n < x < \dfrac{12\pi }{6}+2\pi n\ \ ,\ n\in Z\\\\\dfrac{2\pi }{3}+2\pi n < x < 2\pi +2\pi n\ \ ,\ n\in Z$  

На промежутке  $\boldsymbol{[\ 0\ ;\ 2\pi \ ]}$  наименьшим решением будет  

$\bf x=\dfrac{2\pi }{3}\ \ radian\ =120^\circ$      .  

В вариантах ответов даны целые радианы : 1 радиан ≈ 57,3°  ,

2 радиана ≈ 114,6° < 120° ,

3 радиана ≈ 171,9° > 120°  , ...

Наименьшее целое решение (в радианах)  равно  3 радианам .