Предмет: Алгебра,
автор: yanashakalova0
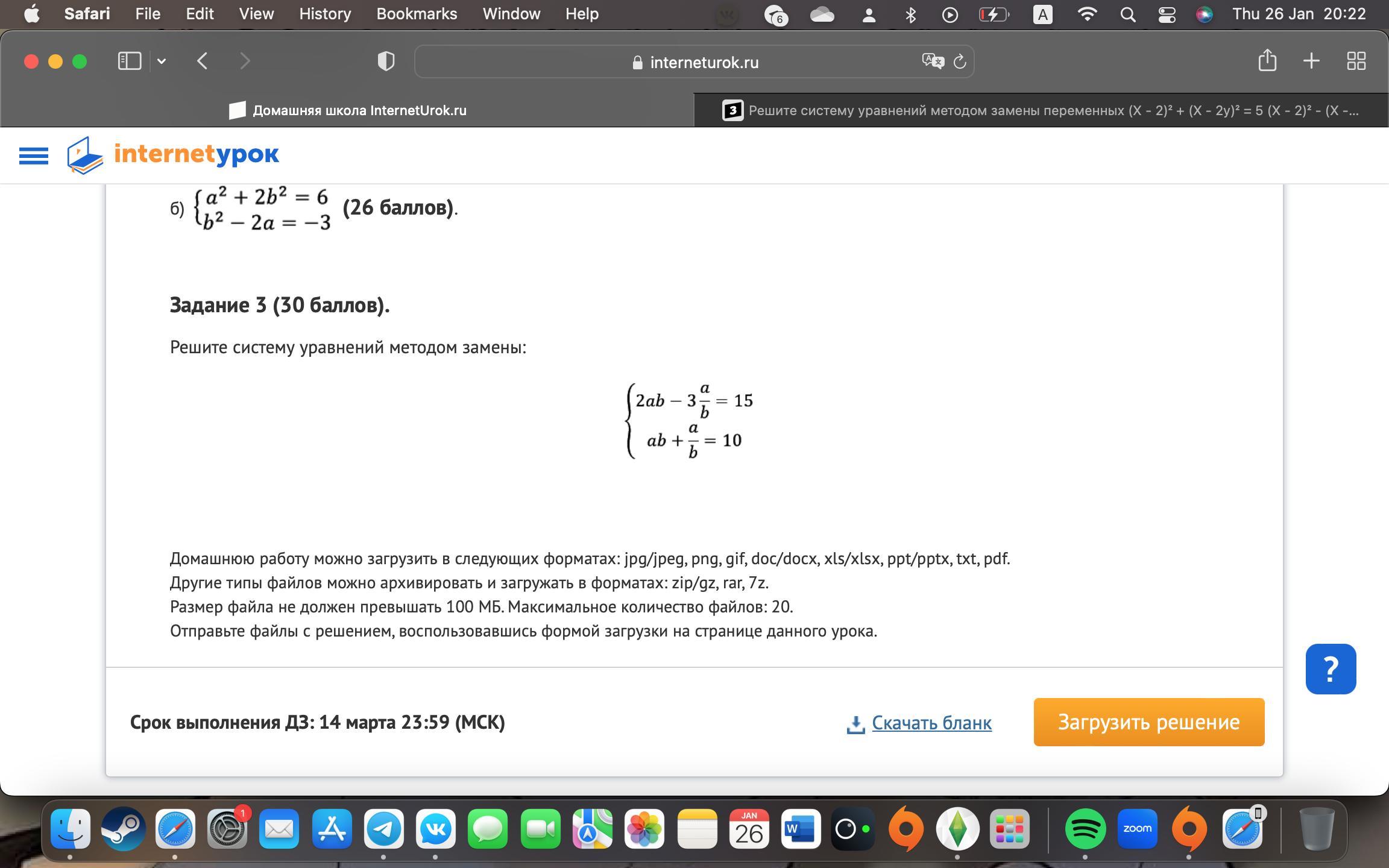
Задание 3 (30 баллов).
Решите систему уравнений методом замены:
Skrinshot 11-10-2021 220603.png
Приложения:
Ответы
Автор ответа:
7
Ответ:
Объяснение:
Решите систему уравнений методом замены:
Сделаем замену:
Тогда получим следующую систему уравнений
Последнюю систему решаем методом подстановки
Сделаем обратную замену
#SPJ1
Похожие вопросы
Предмет: Другие предметы,
автор: Polina20107
Предмет: Геометрия,
автор: Аноним
Предмет: Українська мова,
автор: anastsssiiiaaa
Предмет: Английский язык,
автор: Help993