Предмет: Алгебра,
автор: kermakunovasamira
log3(x²-7)-log3(x-y)=1
помогите пожалуйста решить
Приложения:
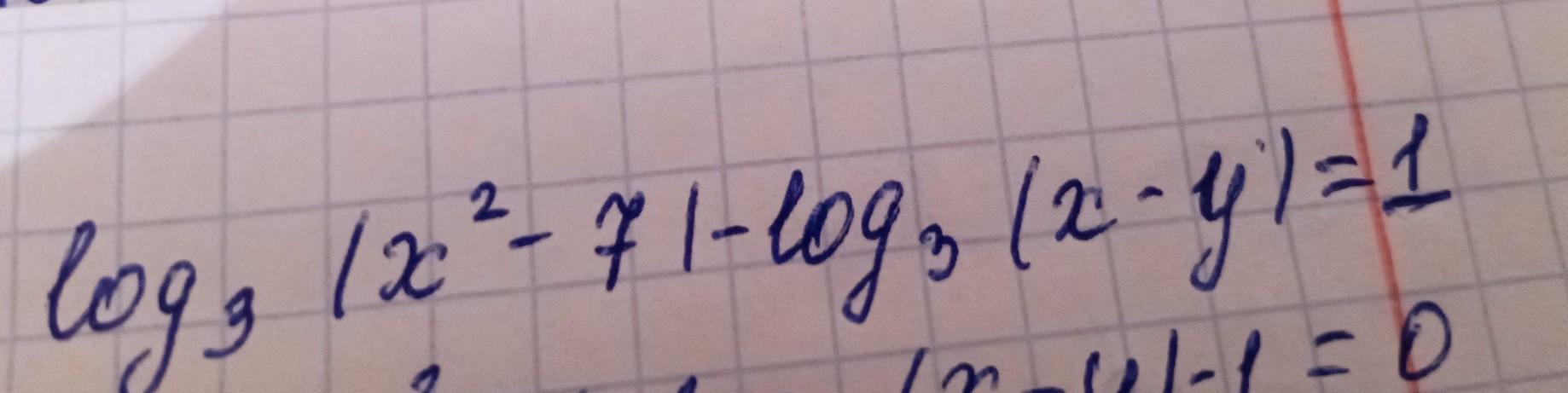
Ответы
Автор ответа:
1
Ответ:
Решением уравнения являются x = 1 и x = 5/2
Объяснение:
Чтобы решить уравнение log3(x²-7) - log3(x-y) = 1, можно начать с изолирования одного из логарифмов на одной стороне уравнения. Мы можем добавить log3(x-y) к обеим сторонам уравнения:
log3(x²-7) = log3(x-y) + 1
Теперь можем поделить обе стороны уравнения на log3(x-y):
(x²-7)/(x-y) = 3
Можем произвести действия с обеими частями уравнения:
x²-7 = 3x-3y
x² - 3x +3y = -4
Произведем дискриминант
D=b²-4ac = (3)² - 4(1)(-4) = 9+16 = 25
Корни уравнения
x1,2 = (3±√25)/2 = (3±5)/2 = 1 или 5/2
x-y = 3
x = y + 3
Таким образом решением уравнения являются x = 1 и x = 5/2
Обратите внимание, что x не должно быть равно y, иначе знаменатель в уравнении будет равен нулю.
Похожие вопросы
Предмет: Литература,
автор: Milashkaarrrrrrrrrrr
Предмет: Алгебра,
автор: evgeniapavlij497
Предмет: Английский язык,
автор: kamilla16062010
Предмет: Русский язык,
автор: milenabikmeeva9
Предмет: Русский язык,
автор: sulejmanovalimbek