Предмет: Алгебра,
автор: vaiti
Найти производную функции
Приложения:
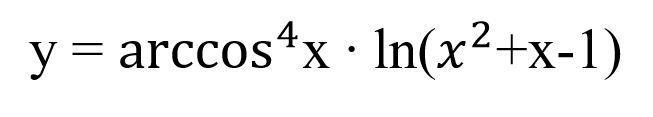
Ответы
Автор ответа:
0
Ответ:
Найдём производную произведения по формуле .
vaiti:
Можете объяснить, откуда -1/корень 1-x^2 появилось?
это производная от функции arccosx , которая является внутренней функцией для степенной функции y=(arcosx)^4 .
Похожие вопросы
Предмет: Химия,
автор: mkarnauh54
Предмет: Химия,
автор: solomenkorish
Предмет: Алгебра,
автор: reygen
Предмет: Другие предметы,
автор: loveayazhan5
Предмет: Обществознание,
автор: valera228333777