Предмет: Математика,
автор: SeverS1de
знайдіть первісну функції графік якої проходить через точку А:


Приложения:
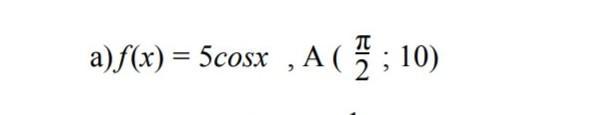
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Найти первообразную функции, график которой проходит через точку А(π/2; 10)
Формула
Найдем С, подставим координаты А(π/2; 10):
Искомая первообразная равна:
Похожие вопросы
Предмет: Математика,
автор: choimariya11
Предмет: Алгебра,
автор: fiwodyl6
Предмет: Английский язык,
автор: veronikatomasevich15
Предмет: ОБЖ,
автор: loopomogite849645
Предмет: Математика,
автор: igorkoksharov00