Предмет: Геометрия,
автор: andrianabelatinskaa
ОЧЕНЬ СРОЧНО ДАЮ 50 БАЛОВ
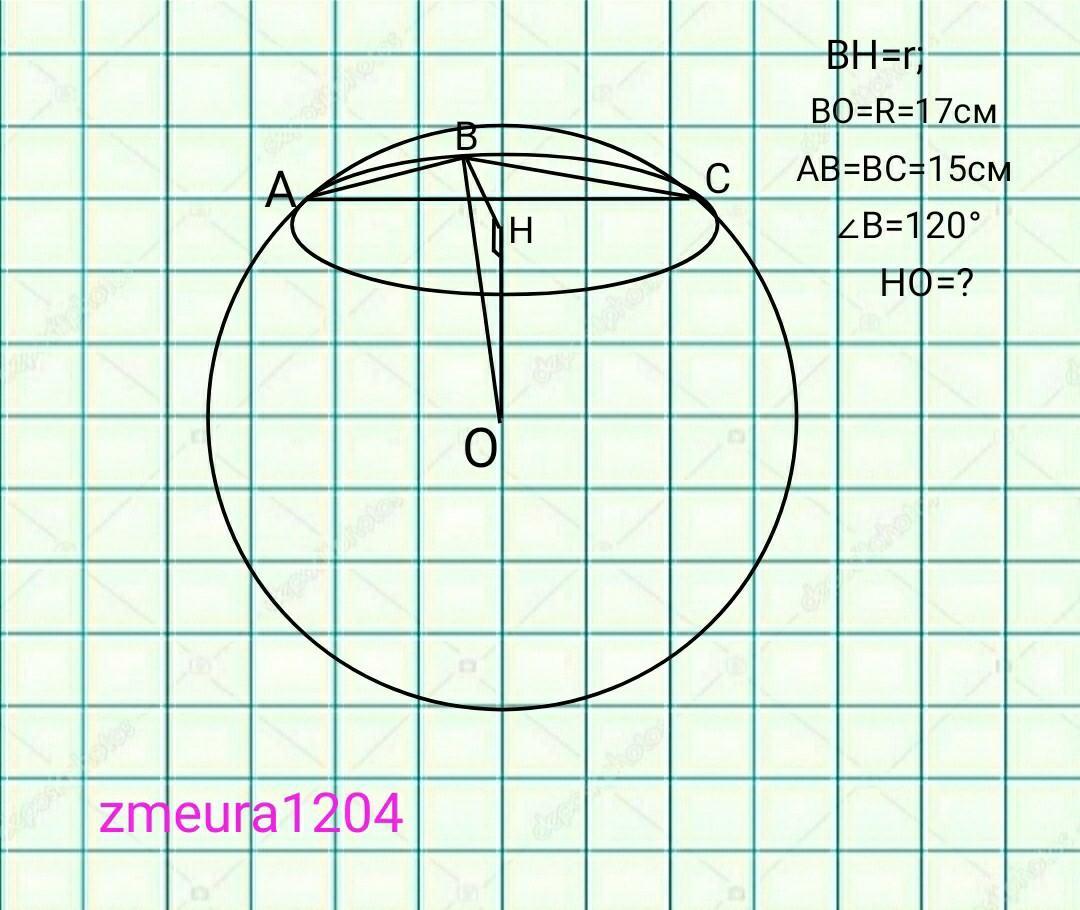
На поверхні кулі позначено точки A, B, C такі, що AB = BC = 15 см, угол АВС=120*. Знайдіть відстань від центра кулі до площини ABC, якщо радіус кулі дорівнює 17 см.
Відповідь: ... см.
Ответы
Автор ответа:
3
Ответ:
Відстань від центра кулі до площини трикутника дорівнює 8см
Объяснение:
За теоремою косинусів:
АС=√(АВ²+ВС²-2*АВ*ВС*cos∠B)=
=√(15²+15²-2*15*15*cos120°)=
=√(225+225-2*225*(-½))=√675=√(225*3)=
=15√3 см сторона трикутника.
r=AC/(2*sin∠B)=15√3/(2*sin120°)=
=15√3/(2*√3/2)=15см (ВН=15см)
∆ОВН- прямокутний трикутник.
За теоремою Піфагора:
НО=√(ОВ²-ВН²)=√(17²-15²)=√(289-225)=
=√64=8см
Приложения:
Похожие вопросы
Предмет: Физика,
автор: marko7091
Предмет: Физика,
автор: marko7091
Предмет: Экономика,
автор: sun5h11ne
Предмет: Українська мова,
автор: Ylia3004