Предмет: Алгебра,
автор: anelprincess69
диагонали параллелограмма равны d1 и d2 а меньшая сторона а. Найдите угол между его диагоналями
d1=4 м, d2=2√3, а=1м
Ответы
Автор ответа:
6
Ответ:
Угол между его диагоналями равен 30°.
Объяснение:
Диагонали параллелограмма равны d₁ и d₂, а меньшая сторона а. Найдите угол между его диагоналями, если
d₁ = 4 м, d₂ = 2√3 м, а = 1 м.
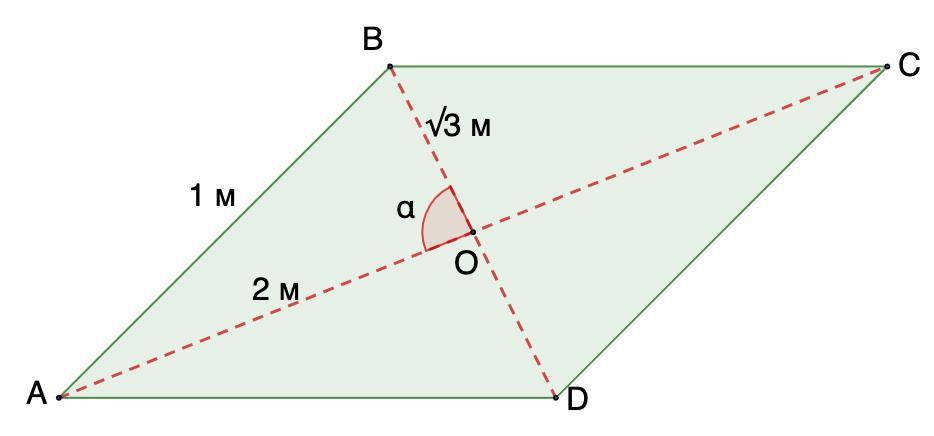
Дано: ABCD - параллелограмм;
АС ∩ BD = O - диагонали;
АВ = 1 м; АС = 4 м; BD = 2√3 м.
Найти: ∠АОВ
Решение:
Рассмотрим ΔАВО.
- Диагонали параллелограмма точкой пересечения делятся пополам.
⇒ АО = 4 : 2 = 2 (м); ВО = 2√3 : 2 = √3 м
Воспользуемся теоремой косинусов:
- Квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон, умноженное на косинус угла между ними.
⇒ АВ² = АО² + ОВ² - 2 · АО · ОВ · сos α
1 = 4 + 3 - 2 · 2 · √3 · cos α
-4√3 · cos α = -6 |: (-4√3)
⇒ α = 30°
Угол между его диагоналями равен 30°.
#SPJ1
Приложения:
Похожие вопросы
Предмет: История,
автор: karinakostucenko0
Предмет: Математика,
автор: gilyazhedinovegor963
Предмет: Геометрия,
автор: limanm
Предмет: История,
автор: technodom999pp