Предмет: Математика,
автор: rostislavstrelkov
Найти решения уравнения
cos (x-π/4)=√3/2 на промежутке
[-π/2;π]
Приложения:
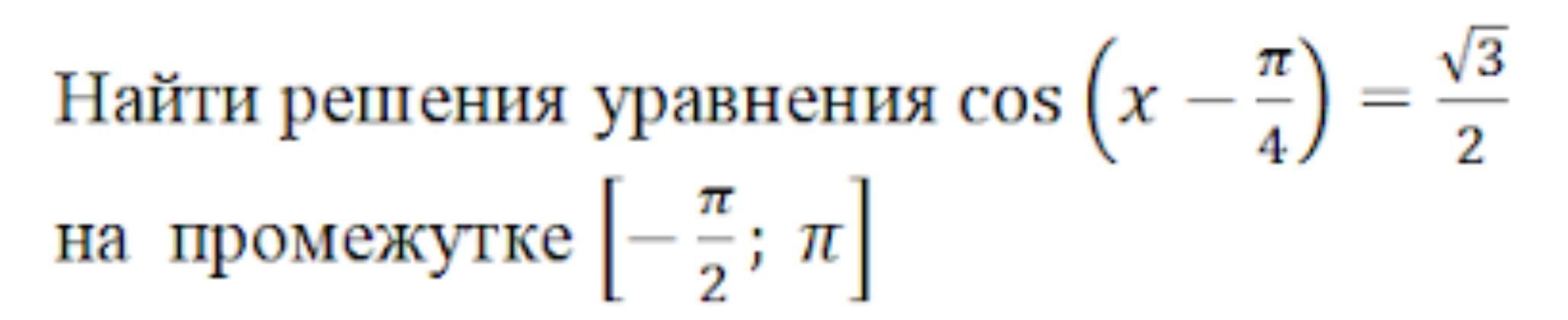
Ответы
Автор ответа:
0
Ответ:
Тригонометрическое уравнение
Промежутку принадлежат корни
.
Похожие вопросы
Предмет: Алгебра,
автор: sht33p
Предмет: Биология,
автор: youryuo34
Предмет: Биология,
автор: alihandro2906
Предмет: Русский язык,
автор: nikitaivanow