Решите пожалуйста, срочно.
Даю 20 баллов

Ответы
Ответ:
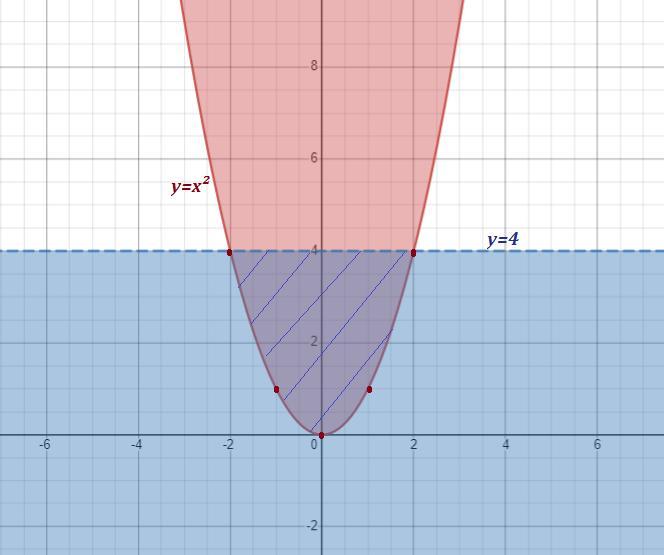
- это множество точек плоскости, лежащих внутри параболы у=х² , граница параболы входит в это множество .
y<4 - это множество точек плоскости, лежащих ниже прямой у=4 , сама прямая не входит в это множество .
Пересечение заданных множеств - это множество точек плоскости, лежащих внутри параболы у=х² , но ниже прямой у=4 . Область на рисунке заштрихована .
2) Диагональ прямоугольника = 13 см , площадь = 60 см² . Найти стороны .
Одна сторона = х см , вторая сторона = у см .
Составим систему уравнений .
Подставим значения х во второе уравнение, получим значения переменной у . Причём отрицательные значения подставлять не будем, так как длины сторон не могут иметь отрицательные значения .
Стороны прямоугольника равны 5 см и 12 см .