Предмет: Алгебра,
автор: cronplay
Для функції f(x)=tgxctgx-2cosx/2 знайти первісну графік якої проходить через точку A(2п,2п)
aarr04594:
А(2п; 2п) . Точно такий запис?
Уточніть умову. cosx/2, це половини кут ?cos(x/2)?
Краще фото.
наверное да, это логичнее, сейчас переделаю))
Кожен читає умову, як бачить.
по суті, якби косинус половинного кута, потрібно було взяти кут косинуса в дужки, а так, "здогадуйтесь самі"...
Ответы
Автор ответа:
3
предлагаю для начала упростить функцию
теперь находим общий вид первообразных этой функции
подставляем F(x) = 2π, x = 2π
2π - sin (2π) + C = 2π
0 + C = 2π - 2π
C = 0
F(x) = x - sin x
2) если делитель два относится исключительно к х:
находим общий вид первообразных этой функции
подставляем F(x) = 2π, x = 2π
2π - 4sin(2π/2) + C = 2π
-4sin π + C = 2π - 2π
C = -4*0
C = 0
F(x) = x - 4sin(x/2)
Автор ответа:
3
Відповідь: фото
Пояснення:
розв'язання завдання додаю
Приложения:
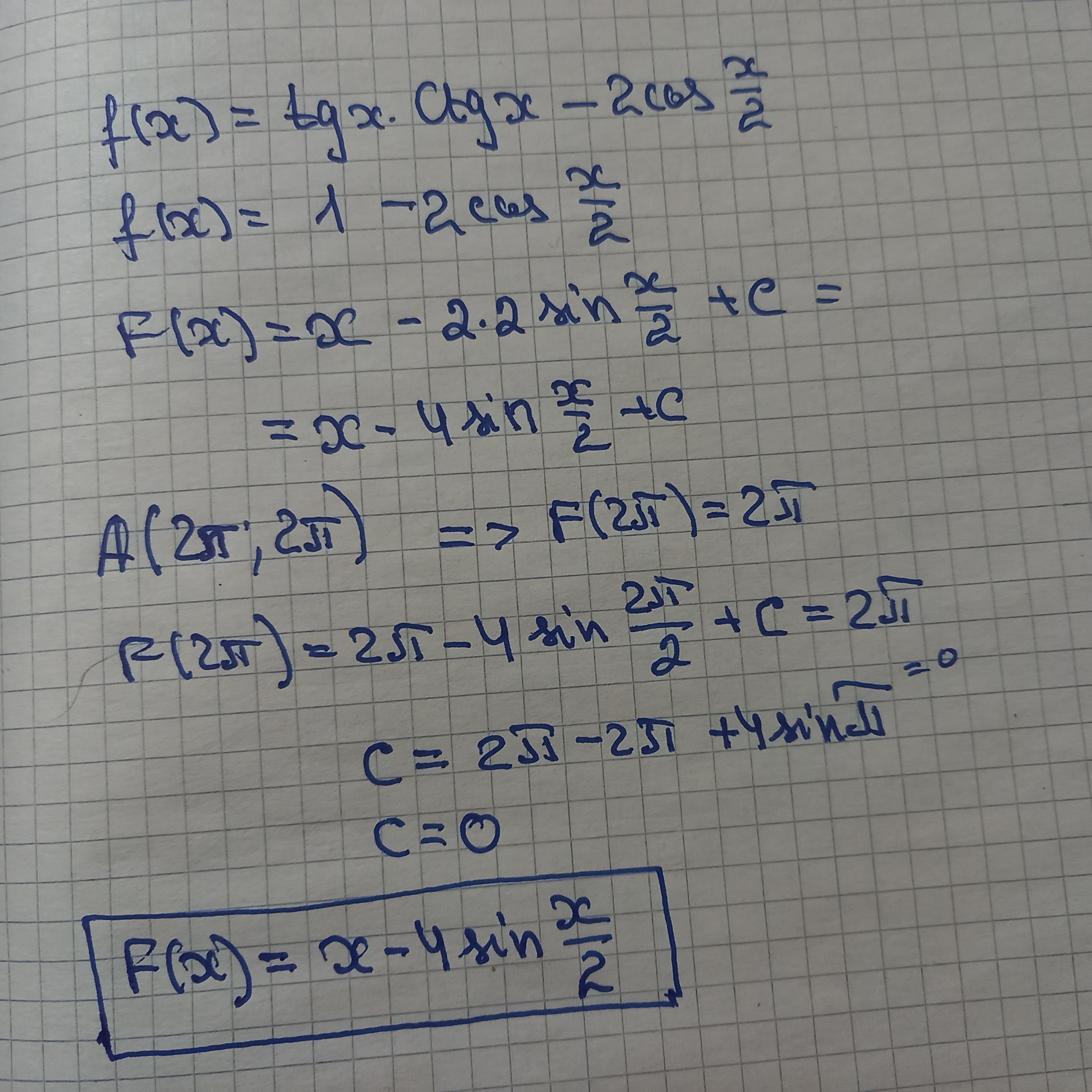
якщо не складно можете зробите ще завдання
https://znanija.com/task/51592652
Похожие вопросы
Предмет: Литература,
автор: Misqueenflower
Предмет: Физика,
автор: lbfyfft
Предмет: Русский язык,
автор: abadalova266
Предмет: Алгебра,
автор: vinogradmulti
Предмет: Английский язык,
автор: svpearl