Предмет: Геометрия,
автор: sambovneiyt66
Помогите пожалуйста сделать задание по геометрии нигде не могу найти решение
Приложения:

<1=<2,как соответственные,поэтому прямые параллельны
Ответы
Автор ответа:
1
Ответ:
Доказано, что a || b.
Объяснение:
Доказать, что если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Дано: прямые а и b; с - секущая.
∠1 = ∠2.
Доказать: a || b.
Доказательство:
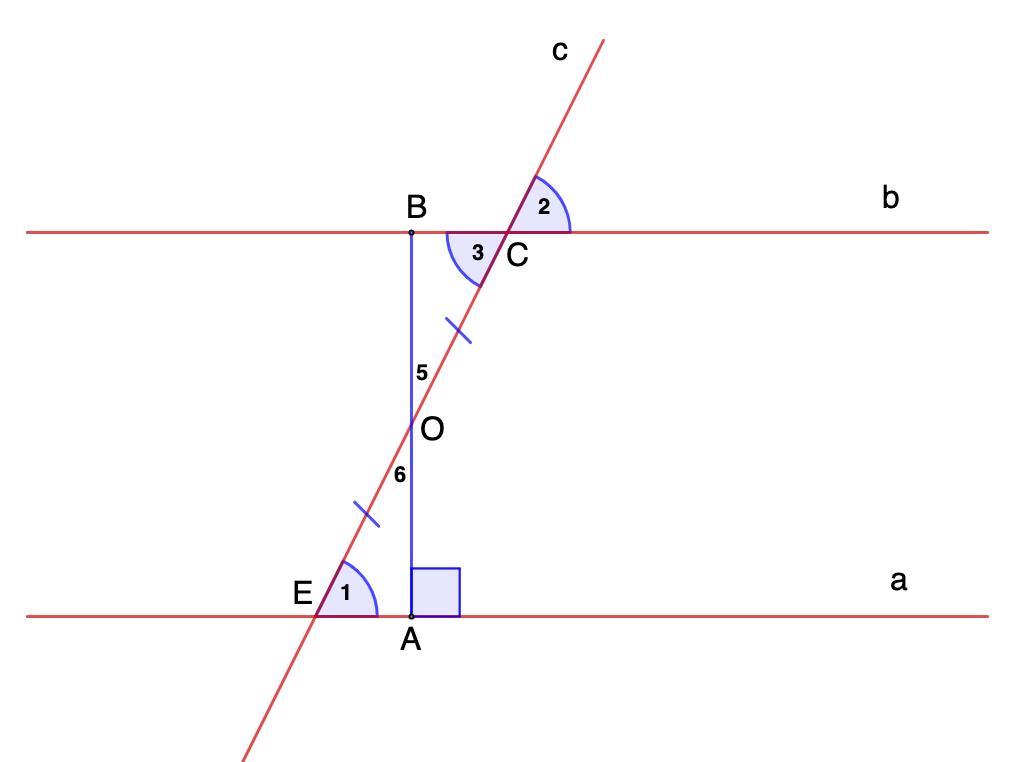
Отметим точку О - середину отрезка СЕ. Опустим из точки О перпендикуляр на а. Точку пересечения обозначим А. Продлим перпендикуляр до b и поставим точку В.
1. ∠1 = ∠2 (условие)
- Вертикальные углы равны.
⇒ ∠3 = ∠2
- Если правые части равенств равны, то равны и левые.
⇒ ∠1 = ∠3
2. Рассмотрим ΔЕОА и ΔОВС.
ЕО = ОС (построение)
∠1 = ∠3 (п.1)
∠5 = ∠6 (вертикальные)
⇒ ΔЕОА = ΔОВС (по стороне и двум прилежащим к ней углам, 2 признак)
- В равных треугольниках против равных сторон лежат равные углы.
⇒ ∠ЕАО = ∠ОВС = 90°.
3. АВ ⊥ а; АВ ⊥ b.
Если две прямые перпендикулярны третьей, то они параллельны между собой.
⇒ a || b.
#SPJ1
Приложения:
Похожие вопросы
В условии задачи дано, что соответственные углы равны.
Нужно немного поднапрячься и подумать, что из этого следует.