Дано функцію  , побудуйте її графік та знайдіть: 1) Область визначення функції 2) Проміжки зростання або спадання функції 3) Область значень функції
, побудуйте її графік та знайдіть: 1) Область визначення функції 2) Проміжки зростання або спадання функції 3) Область значень функції
Ответы
Ответ:
1)D(y) = (-2;+∞)
2)f(x) возрастает на промежутке (-2;+∞)
3)E(y) = (-∞;+∞)
Пошаговое объяснение:
Нужно использовать некие преобразования для графика функции y = f(x) по алгоритму:
Функцию вида y = f(x+a) можно получить , сделав параллельный перенос графика функции f(x) вдоль оси OX на |a| единиц вправо , если a<0 , или на |a| единиц влево , если a>0.
Нам дана функция : f(x) = log₃(x+2)
Строим сперво график функции : f(x) = log₃(x)
Найдём нули:
log₃(x) = 0
3⁰ = x
x = 1
Построим таблицу для точек , причем при x>0:
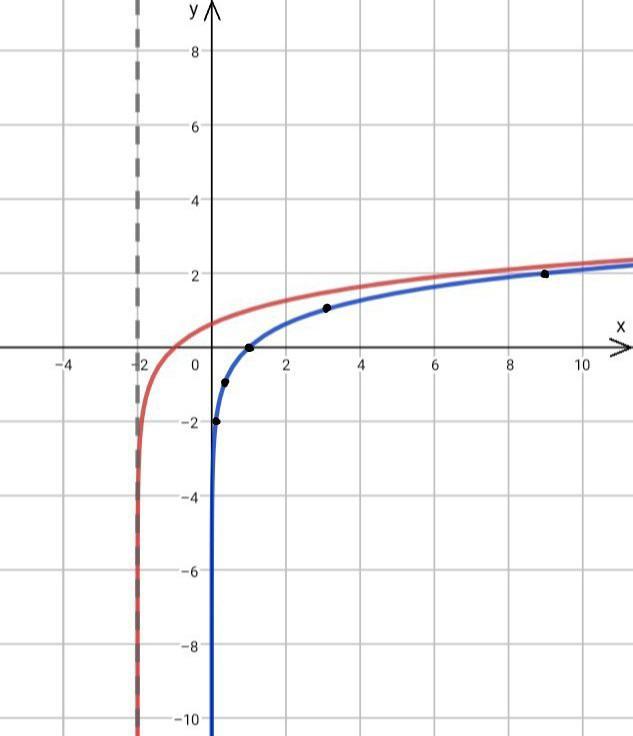
Отмечаем эти точки в системе координат и чертим график функции y = log₃(x) с вертикальной асимптотой x = 0(см.синий график).
Теперь чтобы построить график функции y = log₃(x+2) - нужно каждую точку графика функции y = log₃(x) сдвинуть на 2 единиц влево(так как 2>0). (см.красный график). Таким образом уже асимптотой графика функции y = log₃(x+2) будет являться x = -2.
1) Область определения от точки разрыва до бесконечности , D(y) = (-2;+∞).
2)f(x) возрастает на промежутке (-2;+∞) , промежутка убывания нет.
3)Область значения E(y) = (-∞;+∞)