Question

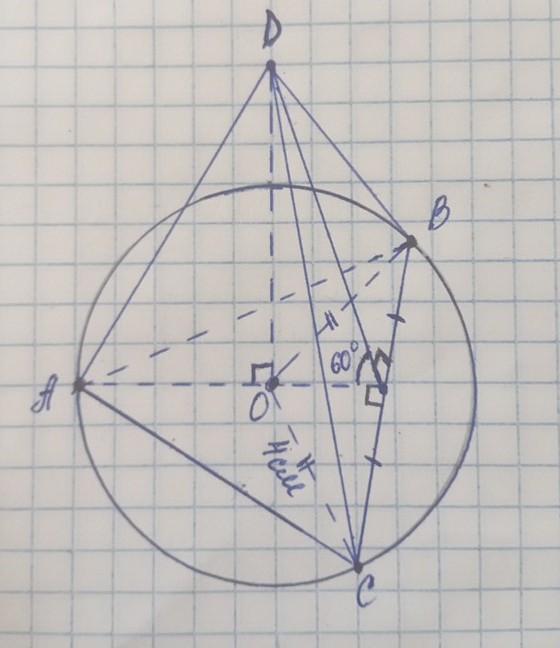
У правильній трикутній піраміді бічні грані утворюють з площиною основи кути 60°, а радіус кола, описаного навколо основи, дорівнює 4см. знайдіть об"єм піраміди

Answer 1

Ответ:

V= 24(см³)

Пошаговое объяснение:

В правильной треугольной пирамиде боковые грани образуют с плоскостью основания углы 60°, а радиус окружности, описанной вокруг основания, равен 4см. найдите объем пирамиды

Дано:

DABC - правильная треугольная пирамида

∠((DBC);(ABC)) = 60°

O - центр оп.окр-ти вокруг основания пирамиды

Rокр. = 4см

Найти: Vпир.

Решение:

Объем пирамиды вычисляется по формуле:

$\boxed{V = \frac{1}{3}S_{osn }\cdot h}$

Где Sосн - площадь основания , h(DO) - высота пирамиды.

Основанием правильной треугольный пирамиды является правильный треугольник , тогда рассм.∆АВС.

Из формулы нахождения радиуса описанной около правильного треугольника окружности найдём a - сторону треугольника:

$\displaystyle R=\frac{a}{\sqrt{3}} \\ \\4 = \frac{a}{ \sqrt{3} } \\ \\ \boldsymbol{a = 4 \sqrt{3} (cm)}$

Найдём площадь ∆АВС по формуле:

$\displaystyle S = \frac{a^2\sqrt{3}}{4}$

Подставим и получим:

$\displaystyle S = \frac{ \left (4 \sqrt{3} \right ) {}^{2} \sqrt{3}}{4} = \frac{ \not16 \cdot3 \sqrt{3} }{ \not4} = 12 \sqrt{3} \left ( cm {}^{2} \right )$

• Угол между плоскостями - это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях. 

Тогда сделаем дополнительное построение: DM⊥BC , АМ , АМ⊥ВС.

Таким образом ∠DМА = 60° - как угол между боковой гранью и основанием . Соединим ОВ , рассм. равнобедренный ∆СОВ , ОМ - является высотой и медианой ⇒ ВМ = СМ = 4√3 : 2 = 2√3(см) , найдём высоту ОМ по т.Пифагора:

OM = √(OC² - CM²) = √(4² - (2√3)²) = √16 - 12 = √4 = 2(см).

Теперь рассм. прямоугольный ∆DOM . Найдём DO через тангенс острого угла:

tg∠DMO = DO/OM

tg60° = DO/2

DO = 2√3(см).

Наконец найдём объем пирамиды:

$\displaystyle V=\frac{1}{\not3}\cdot \not12\sqrt{3}\cdot 2\sqrt{3} = 4\cdot 2 \cdot 3 = 24(cm³)$