помогите с алгеброй пожалуйста
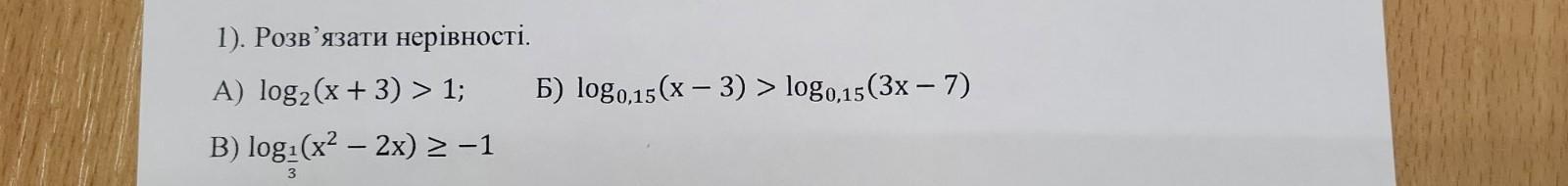
Ответы
Ответ:
1. А) х ∈ (-1; +∞)
Б) х ∈ (3; +∞)
В) х ∈ (-∞; -1] U [3; +∞)
Пошаговое объяснение:
ОДЗ: х + 3 > 0
х > -3
Так как по свойству логарифмов , то:
Так как основание логарифмов больше единицы, то знак неравенства не меняется.
х + 3 > 2
x > -1
С учетом ОДЗ запишем ответ.
Ответ: х ∈ (-1; +∞)
Б)
ОДЗ:
x > 3
Так как основание логарифмов меньше единицы и больше нуля, то изменяем знак неравенства на противоположный.
х - 3 < 3x - 7
x - 3x < -7 + 3
-2x < -4 | :(-2)
x > 2
С учетом ОДЗ запишем ответ.
Ответ: х ∈ (3; +∞)
В)
ОДЗ: x² - 2x > 0
x(x - 2) > 0
x ∈ (-∞; 0) U (2; +∞)
, тогда:
Основания логарифмов меньше единицы и больше нуля, поэтому меняем знак неравенства на противоположный.
х² - 2х ≥ 3
х² - 2х - 3 ≥ 0
Находим нули функции:
х² - 2х - 3 = 0
D = 4 - 4 * (-3) = 16
(х + 1)(х - 3) ≥ 0
+ - +
-------------------------●-----------------------------------●--------------------------------->x
-1 3
Неравенство принимает положительные значения в промежутке [-1; 3], тогда с учетом ОДЗ запишем ответ.
Ответ: х ∈ (-∞; -1] U [3; +∞)